2.3.1 浮点数的表示

字数

2420 字

阅读时间

10 分钟

---

一、IEEE754标准的浮点数格式

电气电子工程师学会（简称IEEE）；IEEE754---由IEEE制定的二进制浮点数算术标准，规定了在计算机内部，如何使用二进制表示和运算浮点数
C语言float型(32bit，单精度浮点型)、double型（64bit，双精度浮点型）就是符合IEEE754标准的浮点数格式

在考研大纲中只要求IEEE754标准和浮点数的加/减运算，其中最常考的是 float 型

复习建议：对于不符合IEEE754标准的浮点数格式可少花时间，仅当作思维扩展；且浮点数仅关注加减运算

最重要的题型：真值转浮点数、浮点数转真值

1. 科学计数法

术语：

1. 符号：决定数值的正负
2. 尾数：影响数值的精度。尾数的位数越多，精度越高
3. 阶码：反映小数点的实际位置
4. 基数：K进制通常默认基数为K
5. 规格化：确保尾数的最高位非0数位刚好在小数点之前

2. float与double的格式表示

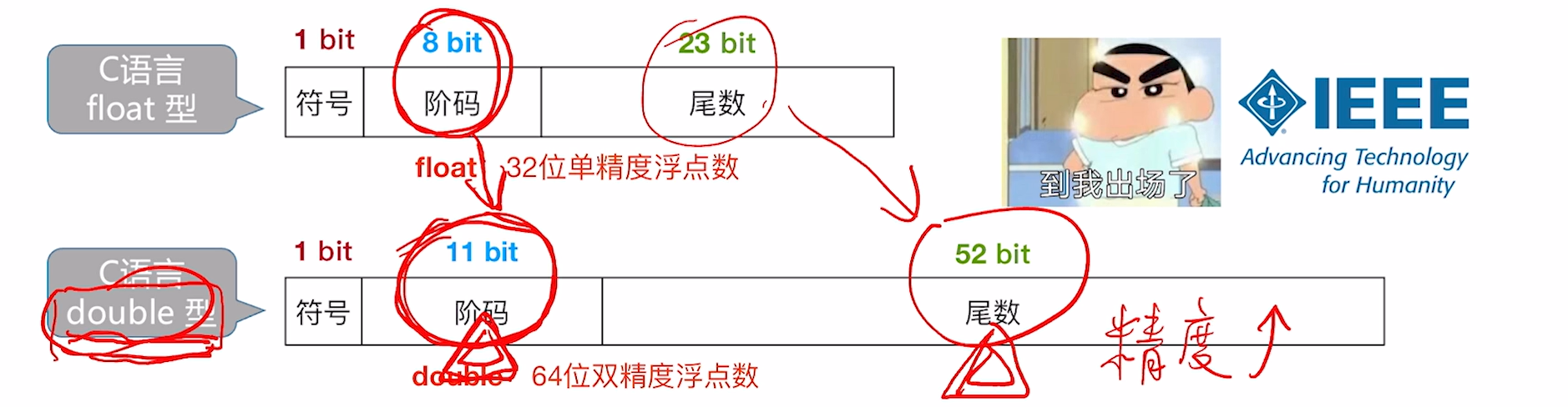
默认基数为 2

3. 🌟float 单精度浮点数的存储（常考）（浮点数转真值）

真值转移码：按“无符号整数”解读真值，再加上偏置值，就得到移码

各部分的存储：

1. 符号：0正 1负
2. 尾数：规定小数点位置在23bit之前。默认存储规格化位数，且小数点前的1省略（隐含）（省略小数点前的1 的好处：增加尾数的实际精度）以原码定点小数的形式进行存储的
3. 阶码：用移码表示，规定偏置值为127
4. 基数：规定基数为2即可，不用专门存储

4. double 双精度浮点数的存储（浮点数转真值）

与float型存储并无二致，仅在移码的偏置值进行修改

各部分的存储：

1. 符号：0正 1负
2. 尾数：规定小数点位置在52bit之前。默认存储规格化位数，且小数点前的1省略（隐含）（省略小数点前的1 的好处：增加尾数的实际精度）以原码定点小数的形式进行存储的
3. 阶码：用移码表示，规定偏置值为1023
4. 基数：规定基数为2即可，不用专门存储

如何记忆移码的偏置值？

记住该偏置值的公式：偏置值=$2^{n-1}-1$，其中 n 为阶码的位数

5. 真值转换为浮点数

6. 复杂小数如何转换为二进制

7. 🌟浮点数的表示范围(需要重点记忆)

IEEE754标准规定：仅当阶码不全为0、也不全为1时，表示这是一个“规格化浮点数” 阶码全为0、全为1留作特殊用途，需要按照特殊方式解读

单精度浮点数float 是重点！！！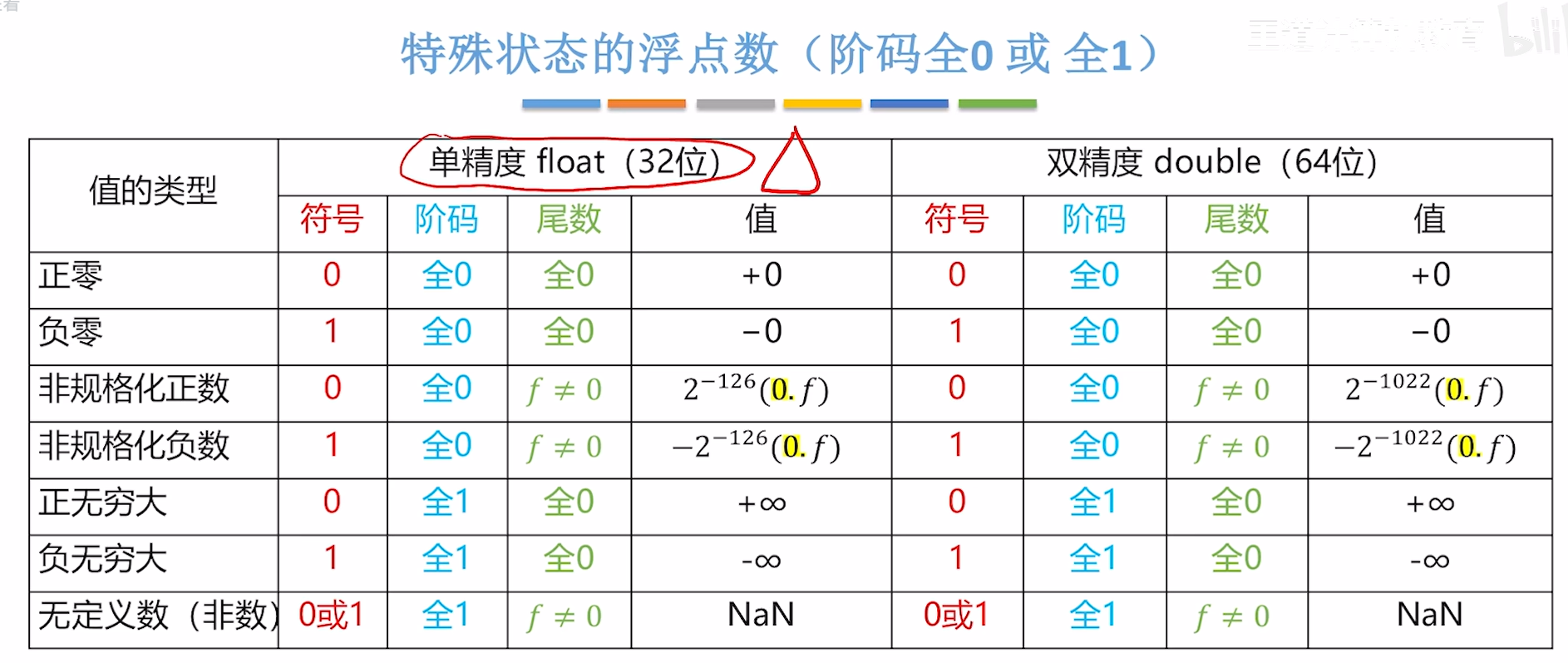

$f\ne 0$ 表示的是：不全为0（f 代表的是尾数）

非规格化数：隐藏位不是1，而是0，即：尾数为0.xxxxx；且单精度浮点数的阶码真值为-126（指数为-126）

阶码的表示范围

阶码（移码表示）的取值范围：1~254 🌟阶码的真值的取值范围：-126~127

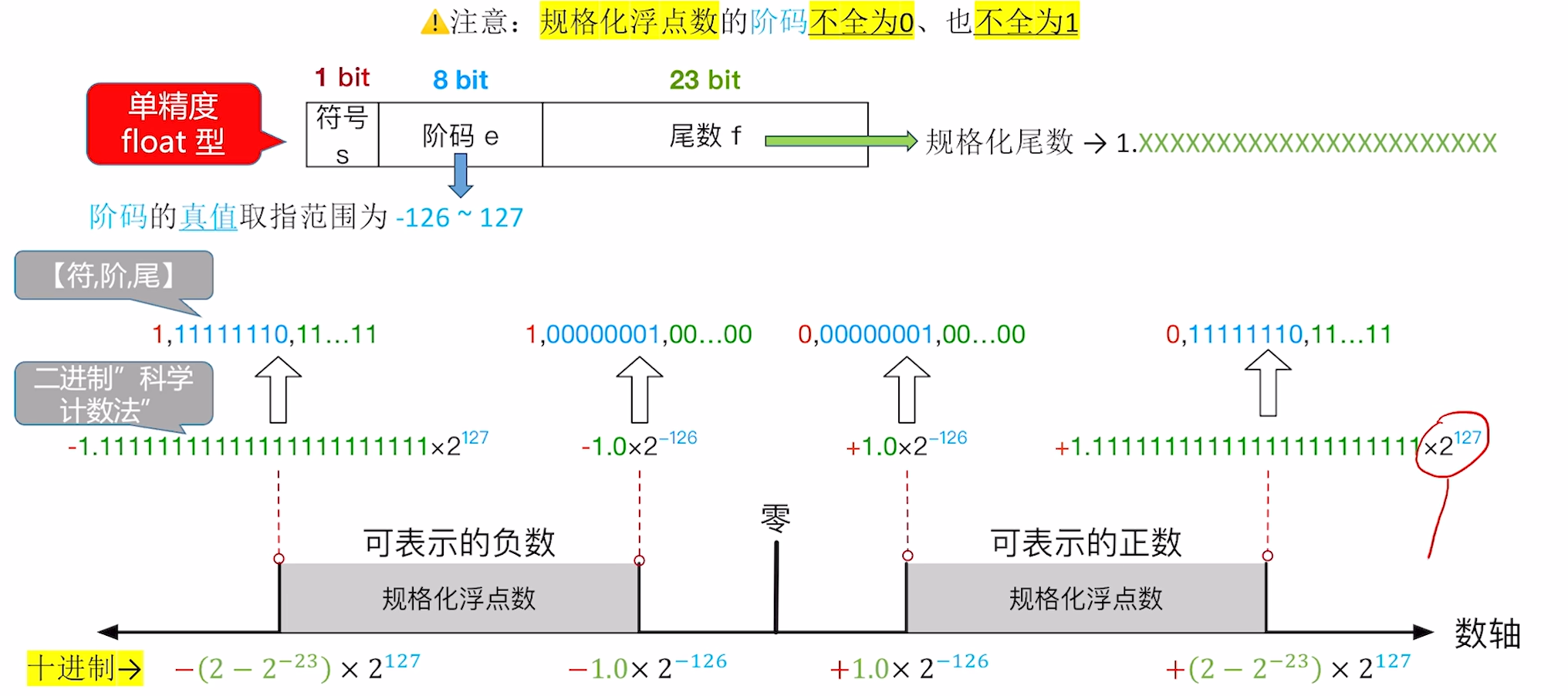
为什么规格化浮点正数显示是 $+(2-2^{-23}\times 2^{127})$ ？ 因为该二进制的值相当于如下二进制减法的结果： $10.000...000-0.00...0001$ ，即：$2-2^{-23}$ (尾数是从 $2^{-1}$ 一直到 $2^{-23}$ )

（1） 浮点数的上溢

运算结果大于最大规格化正数时称为正上溢，小于最小的规格化负数称为负上溢 （数轴最左边和数轴最右边溢出） 正上溢、负上溢统称为上溢（Overflow），也会翻译为“溢出”

浮点数上溢（溢出）的处理：

1. 浮点数运算部件将运算结果设置为 $+\mathrm{\infty }$ 或 $-\mathrm{\infty }$ （参考阶码全1，尾数全0的特殊状态浮点数表）
2. 设置浮点数溢出异常标志位（如：x86会将浮点数运算单元FPU的OE标志位Overflow Exception 置为 1） 注：IEEE754规定，默认不响应浮点数溢出异常，不中断程序，除非程序员手动开启此类异常溢出

（2）浮点数的下溢

下溢范围图示：运算结果在0到最小规格化正数之间时称为正下溢，在0到最大规格化负数之间时称为负下溢。正下溢和负下溢统称为下溢（Underflow）

浮点数运算结果下溢的处理：

1. 若结果落入非规格化区间：用非规格化浮点数存储；若结果太小（真值逼近于0），则按机器零存储
   • 🌟非规格化浮点数的解读：只能按照特殊状态浮点数表（阶码全0、全1）中的内容进行解读
2. 若下溢至机器零，设置浮点数下溢异常标志位 注：IEEE754规定，默认不响应，不中断程序

（3）非规格化浮点数

🌟非规格化浮点数的解读：只能按照特殊状态浮点数表（阶码全0、全1）中的内容进行解读

非规格化浮点数的 $\mathrm{阶}\mathrm{码}\mathrm{真}\mathrm{值}=1-\mathrm{偏}\mathrm{置}\mathrm{值}$，或者也可直接记住其阶码真值（float--> -126；double --> -1022）

（4）非数（NaN）的表示

在IEEE754标准中，NaN 代表 “不是一个数”（Not a Number）

运算结果为NaN的典型例子：

1. 0除以0
2. 负数开根号
3. 无穷减无穷

特别的，非零数值除以0 的结果是无穷

二、数据的存储与排列

1. 大小端模式

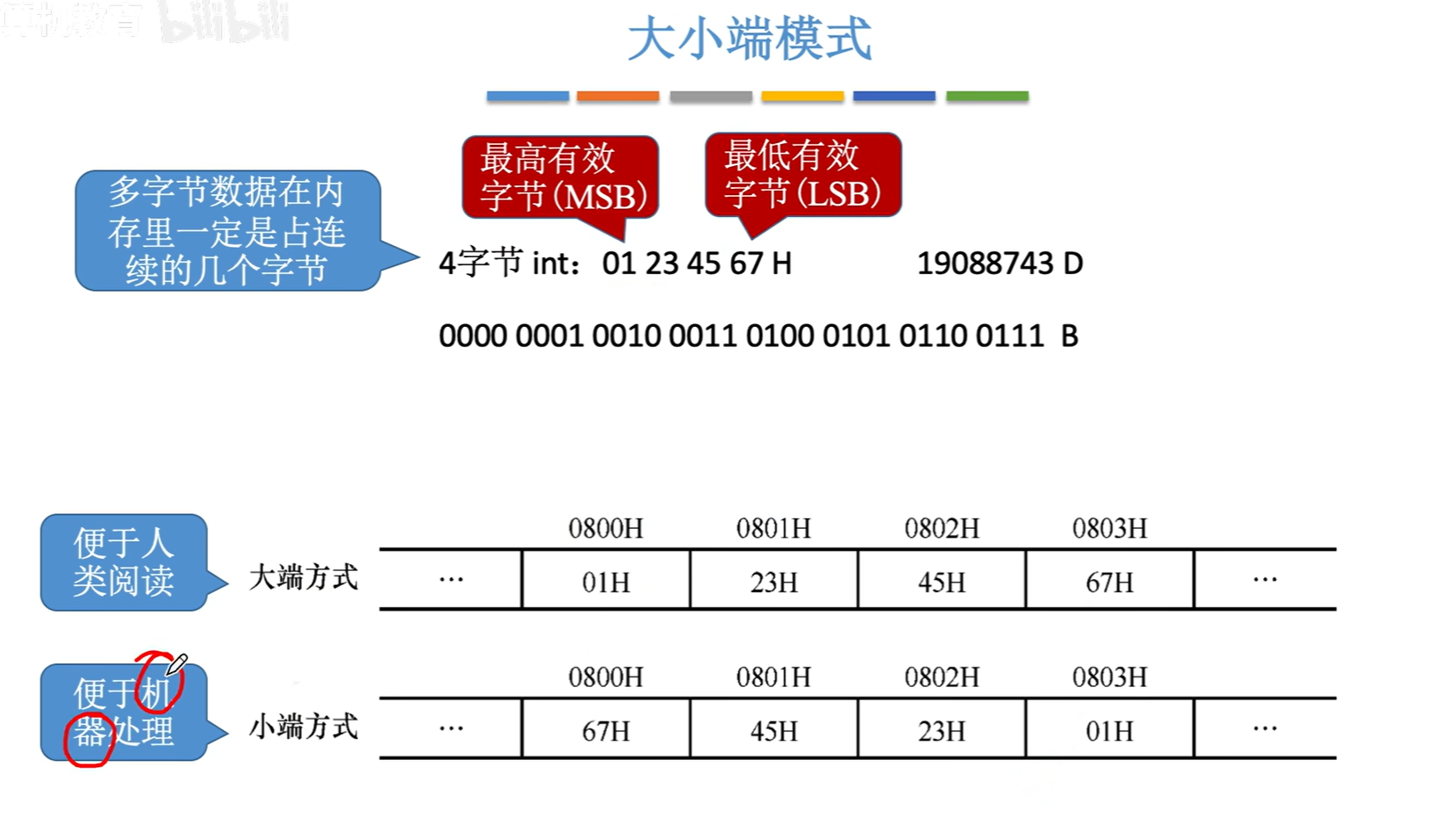大端方式：地址从前往后，从低到高，分别按最高有效字节MSB到最低有效字节LSB的顺序进行存储

小端方式则反过来

2. 边界对齐

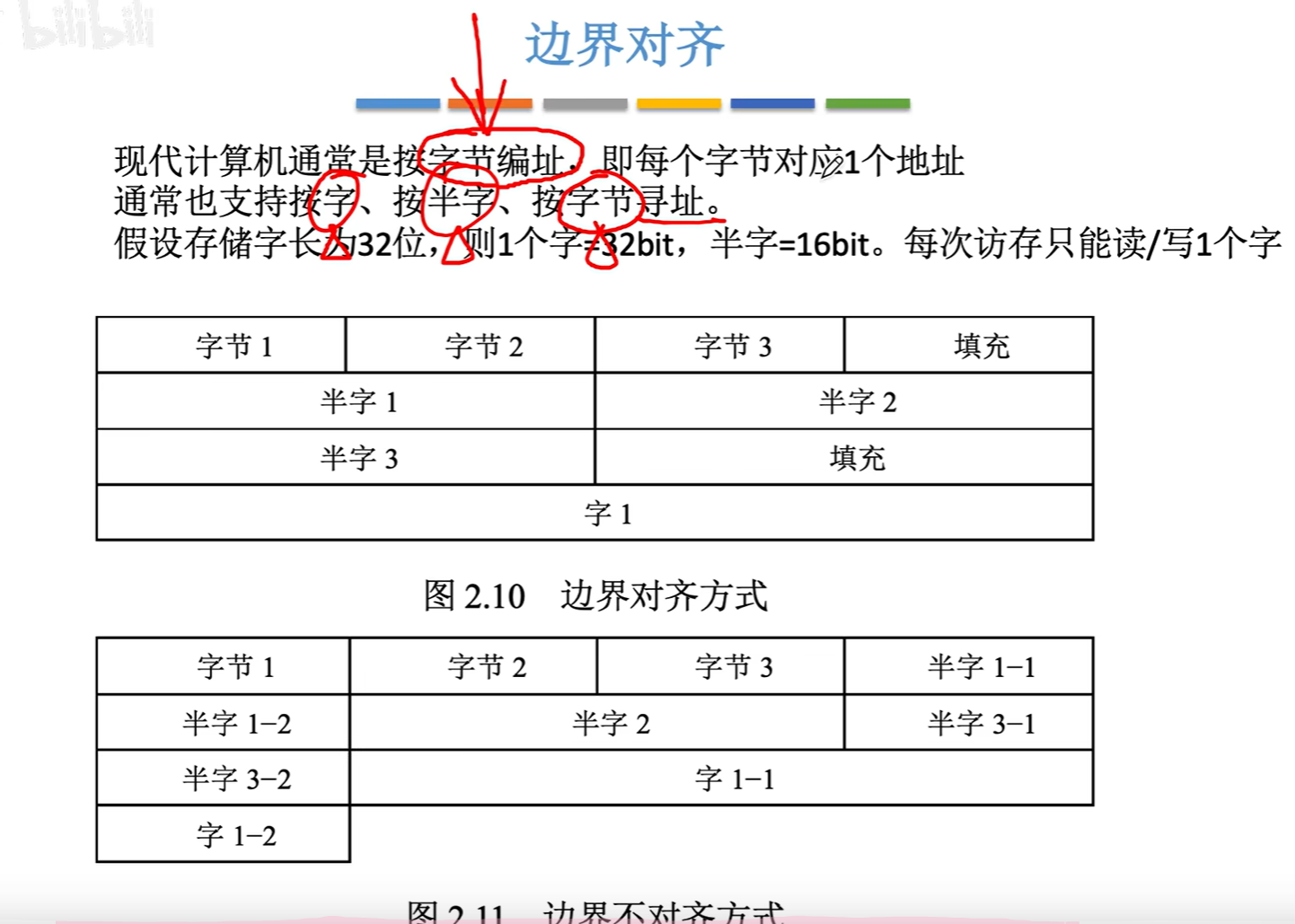
现代计算机通常使用字节编址，每个字节对应一个地址，当然我们也可以按字寻址、按半字寻址、按字节寻址，但最终都需要转化为按字节寻址（下标都从0开始）

因为每次访存只能读写一个字，假设我们现在存储了3个char、3个short和1个int类型的变量，则可使用边界对齐方式和边界不对齐方式来存储

1. 边界对齐方式，在第一行字中，存储3个char类型变量，仅剩余一个字节，不够存储short变量，故将其存储至第二行的半字中，同理：int无法完整存入到第三行的剩余半字，所以将其存入到第四行的字中
   • 这样存储的好处：每个变量只需要1次读/写即可获得
2. 边界不对齐：同样的，在第一行存储3个char变量后，仅剩余一个字节的存储空间，此时不够存储short变量，则我们将该short变量存储的半字拆分为两段，前半段用于填充第一行的最后一个字节，后半段用于填充第二行的前半个半字，这两段组成了一个完整的short变量
   • 这样存储可节省存储空间，但可能需要2次读/写才能得到完整的变量数据

• 区别：
  1. 边界对齐是空间换时间
  2. 边界不对齐是时间换空间

三、浮点数的加减运算

课本P60

步骤：

1. 对阶，使得两个数的阶码相等
2. 尾数加减
3. 尾数规格化：将尾数变化为规格化形式：$\pm 1.\text{x}...\text{x}$
4. 舍入：为保证精度，可能对尾数的保留位数作出要求，以下有四种舍入方式
   1. 就近舍入：若计算结果正好在两个可表示数的中间，即：$xx.xx5$，则选择结果为偶数，如：选择结果为 $1.245$，该结果正好在 $1.24,1.25$ 之间，故选择结果为 $1.24$；其他情况则采用就近舍入（参考四舍五入）
   2. 正向舍入：取右边最近的可表示数（即：朝数轴 $+\mathrm{\infty }$ 方向舍入）
   3. 负向舍入：取左边最近的可表示数
   4. 截断法：直接截取所需的位数，丢弃后边的所有位
5. 溢出判断：浮点数的溢出是由指数上溢来判断的
   1. 指数上溢：指数超过了最大允许值（127或1023）
   2. 指数下溢：指数超过了最小允许值（-149或-1074） （对于非规格化数的情况，当尾数$f$ 为0.00...01 时，指数的最小允许值为-126-23=-149或-1022-52=-1074）

贡献者

freeway348

文件历史

最后编辑于 10 天前查看完整历史

74226-Create 抓阄原理.md