2.2.4 定点数的乘除运算

字数

1455 字

阅读时间

6 分钟

---

无符号数的乘除运算课本中已给出，本章笔记仅补充有符号整数的乘除运算

OF与CF

在计算机中，CF一般仅用于表示无符号整数加减运算是否溢出；而OF可同时用于表示有符号整数和无符号整数乘法是否溢出

一、有符号整数的乘法运算

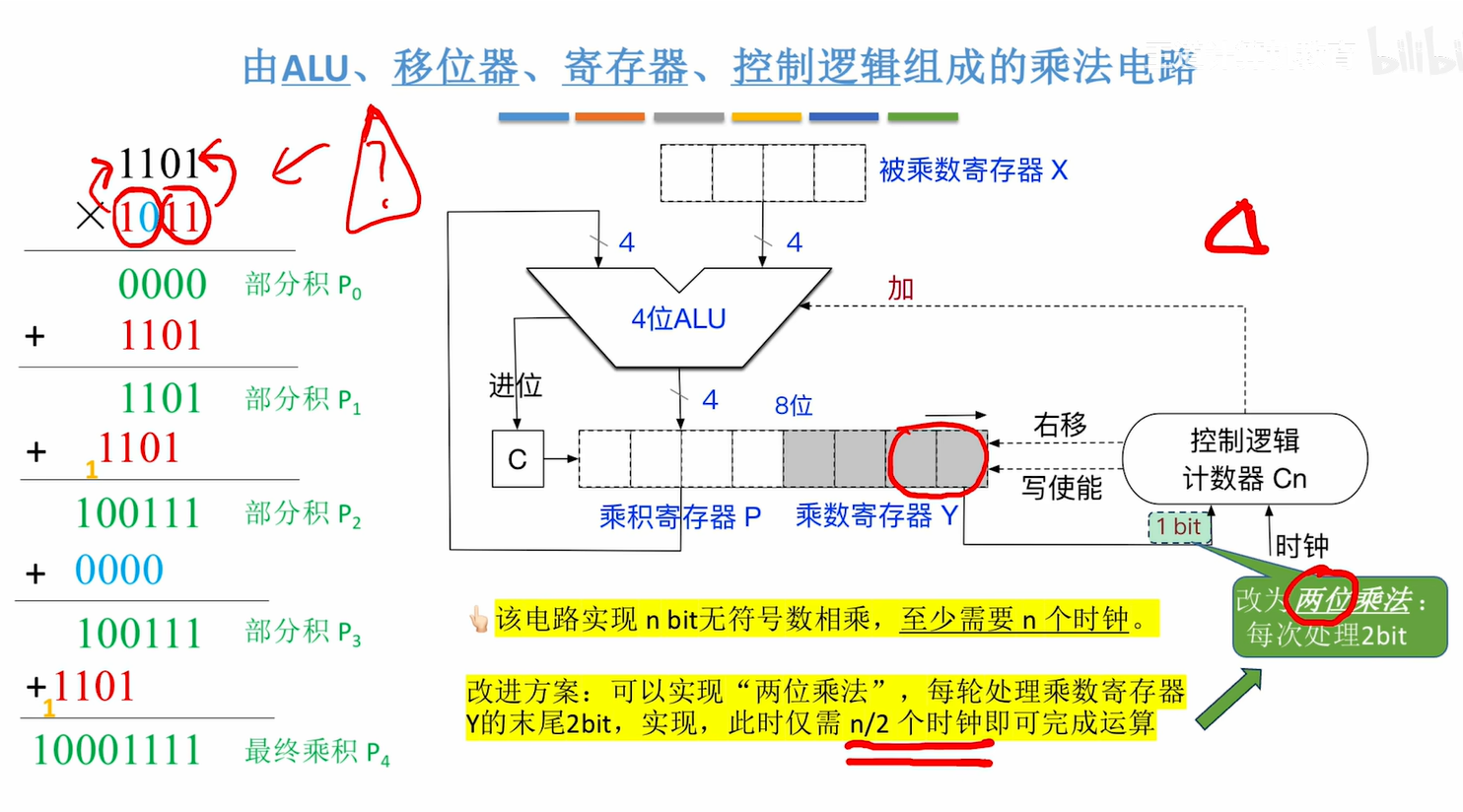
1. 区别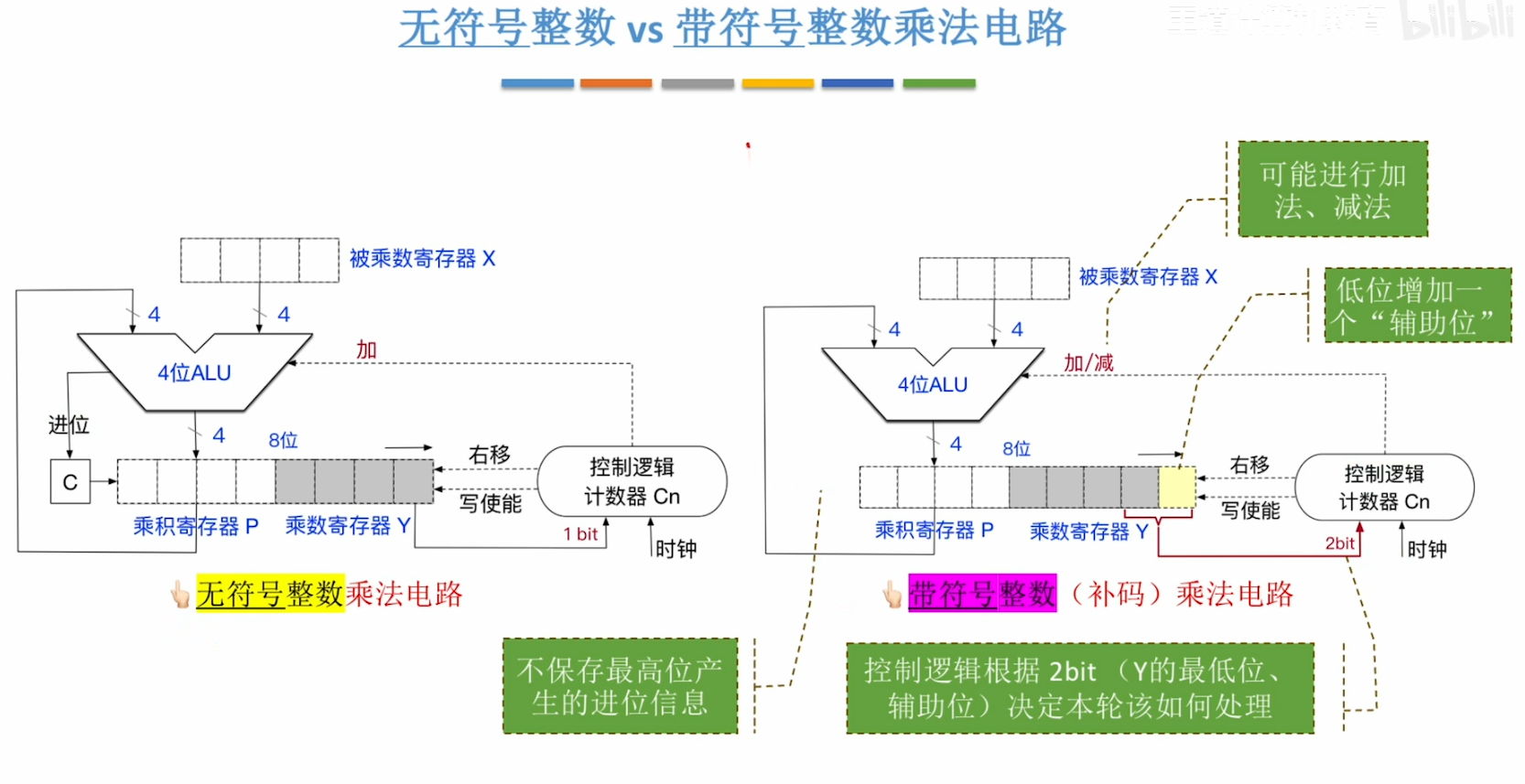： 什么是“写使能”：即：Write Enable “写使能”的作用：由控制逻辑计数器Cn发出"写使能"控制信号，使得控制器P允许被写入 该电路实现n bit 无符号数相乘，至少需要n 个时钟
2. 计算准备步骤：
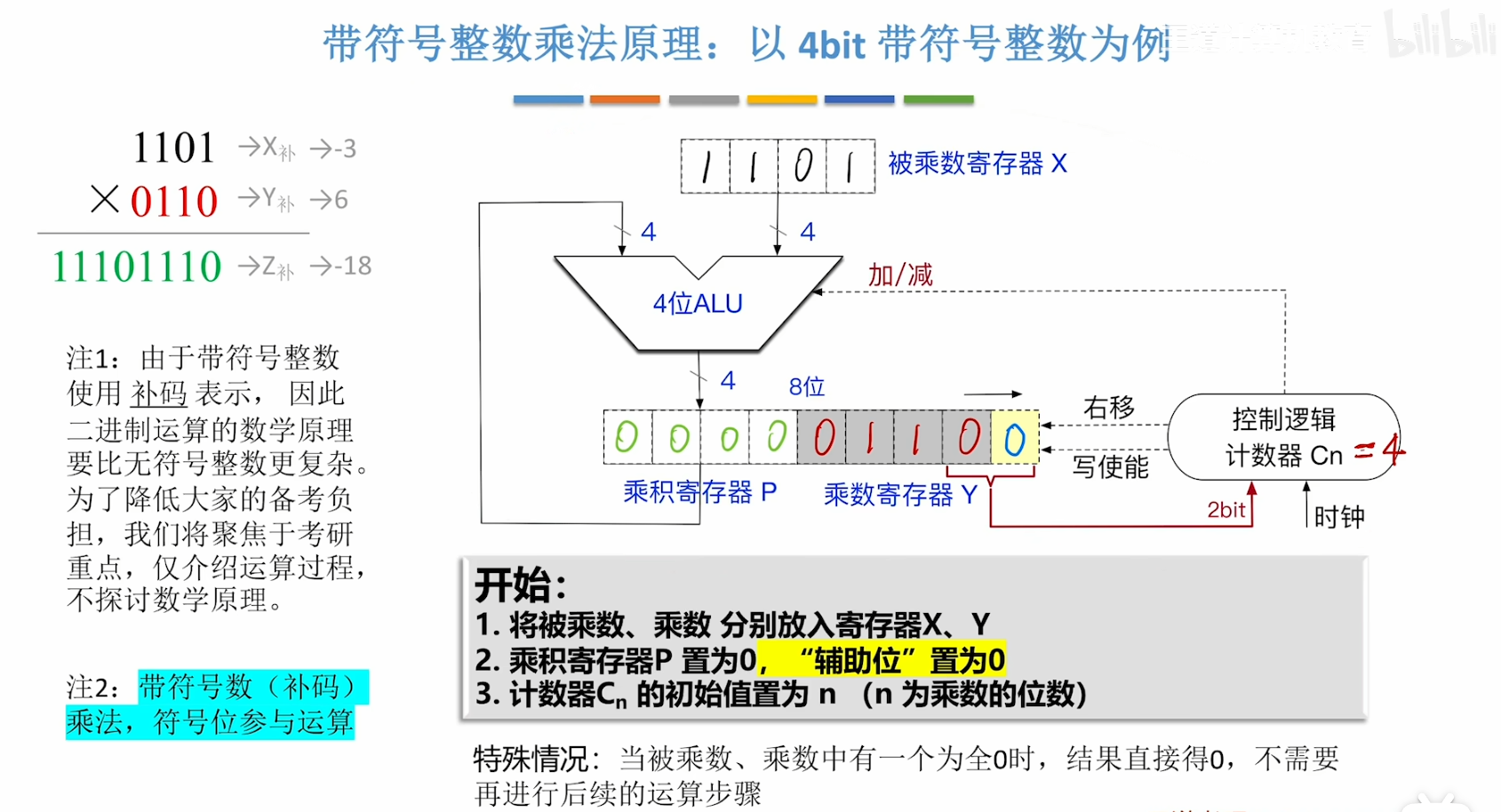
3. 具体计算步骤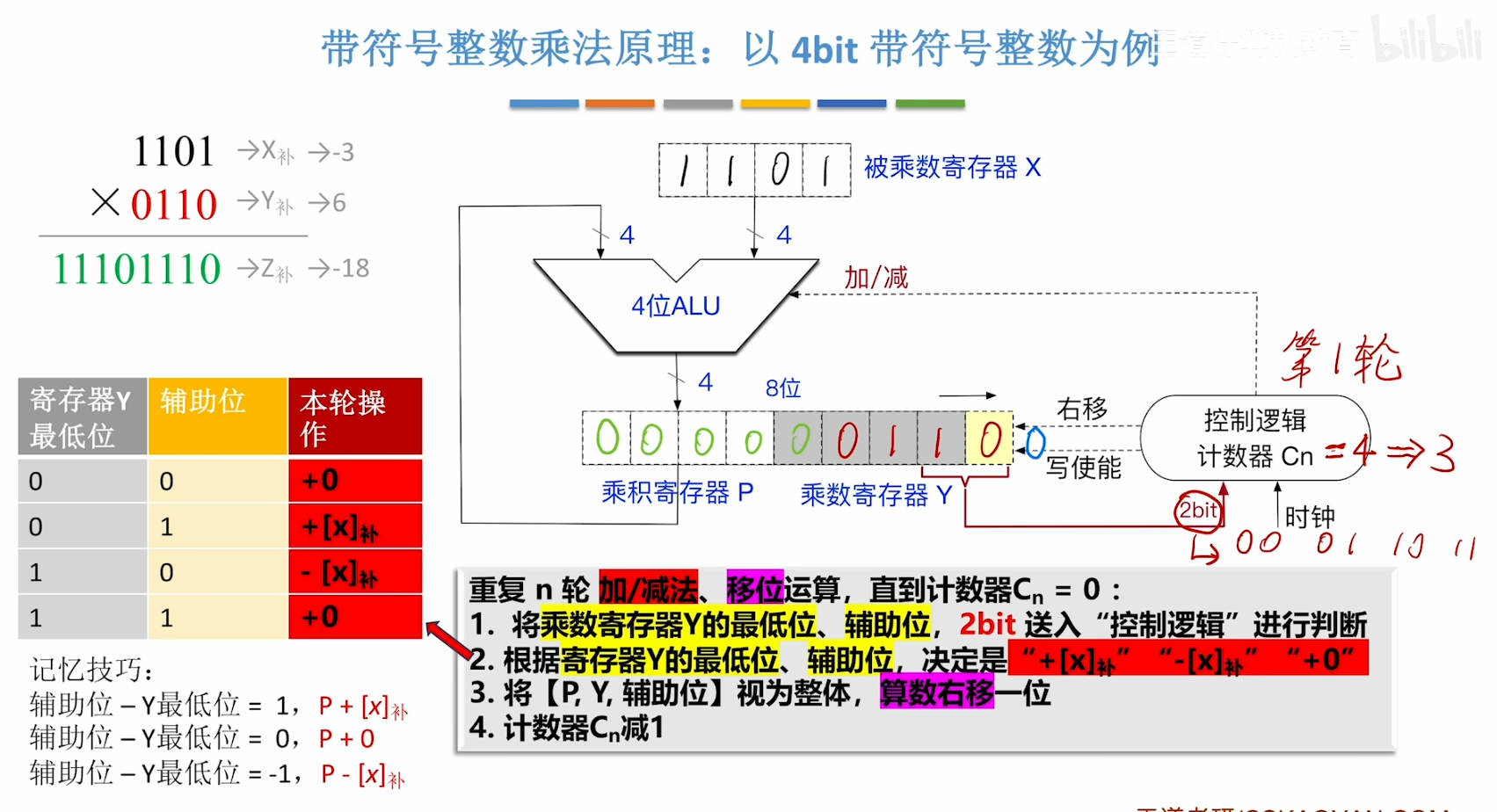： 当 + 0 时，可以什么都不做就直接进入下一步 算数右移后，高位以符号位补足 Cn每次取两位（乘数寄存器Y最后一位+辅助位） 因为寄存器内部存储的机器数就是以补码形式存储的，所以要对部分积 $P_i$ 做计算，就一定要用补码 只要$V=Y_0\oplus \text{辅助位}=1$ 则一定有 $[x{]}_{\mathrm{补}}$，并且本轮操作的符号位是看 $Y_0$ 的：0正1负；其余情况均为+0，即：不进行操作
4. 计算结束：
5. 判断溢出： 若高 n + 1 位（一共有2n位）不完全相同，则说明发生溢出，此时可将OF标志位（溢出标志位）置为 1
   • 为什么是高 n + 1 位？
     • 因为低n位的最高位是符号位，若高n位均与低n位的符号位相同，则补码表示范围正常（因为运算结果只会用2nbit的寄存器暂存，最终只会保留低n位作为计算结果）
6. 溢出的处理：
   1. 忽略溢出，只不过会导致错误的运算结果
   2. 处理溢出：在乘法指令后执行一条溢出自陷指令，该指令会检测OF标志位，若OF==1，则执行操作系统的“异常处理程序”

计算机实现乘法的三种方式

该内容主要在选择题、简答题出现

1. ALU、移位器、寄存器、控制逻辑组成的乘法电路

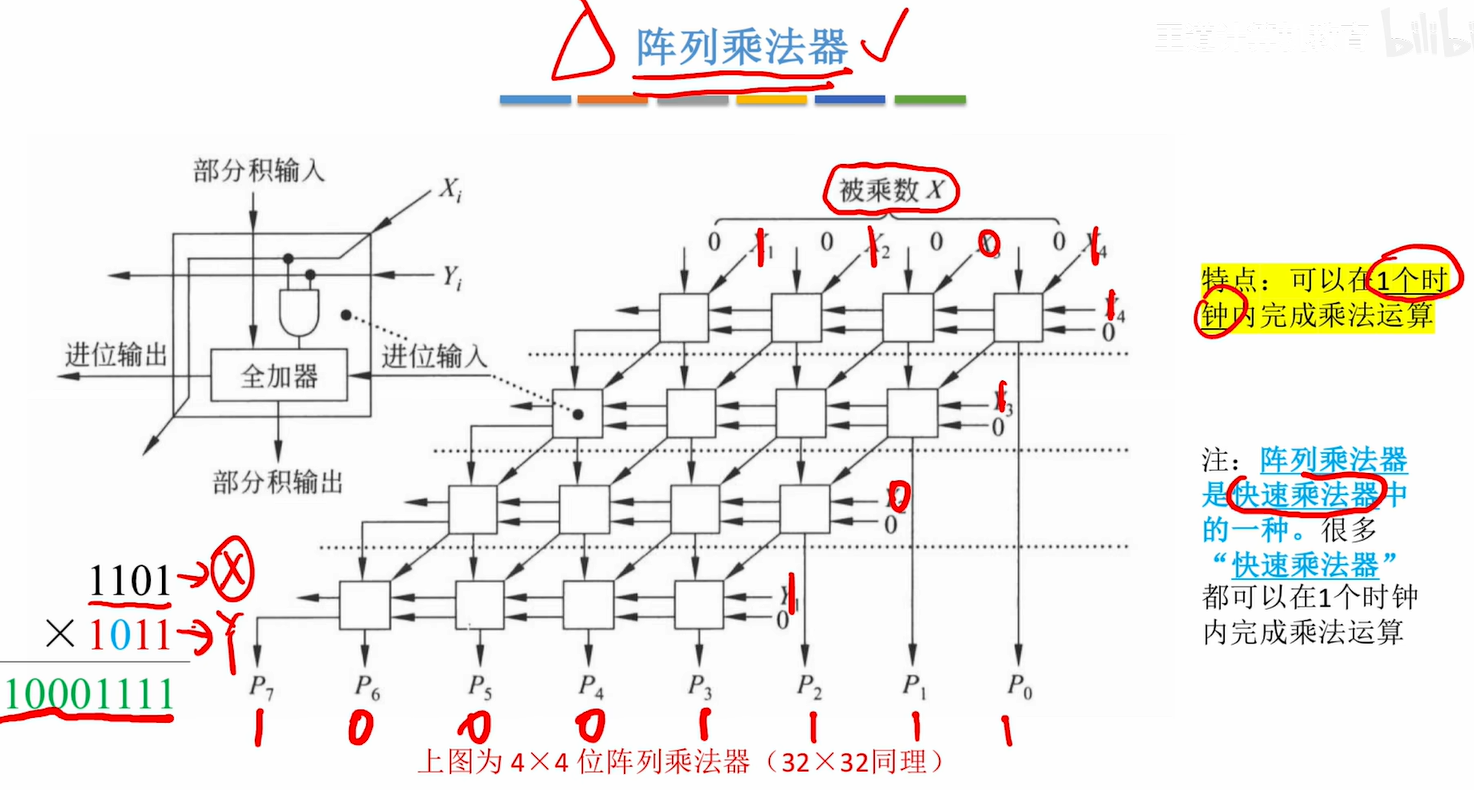
2. 阵列乘法器

3. 逻辑运算、加减运算

我们总能使用位运算、移位运算来实现乘法指令，只不过这种方式运行速度很慢

4. 总结（小题、简答题常考）

在计算机内部，三种实现乘法运算的比对：

1. 阵列乘法器（快速乘法器的一种）的运算速度最快------可在1个时钟内完成运算
2. 由ALU、移位器、寄存器、控制逻辑组成的乘法电路运算速度较快-----通常需要多个时钟（n个时钟：n bit整数的运算）
3. 可以使用移位运算、加/减运算 等效实现乘法（在计算机内部没有乘法运算电路/乘法指令时可用），但运算速度最慢

二、🌟🌟🌟有符号整数的除法运算

除法电路运算中间过程较复杂，复习性价比不高，建议第一轮复习不要死磕运算的中间过程细节，在后几轮复习中若有余力可复习

TIP

建议重点关注：除法电路的开始状态、结束状态、除法异常判断

1. 初步准备：
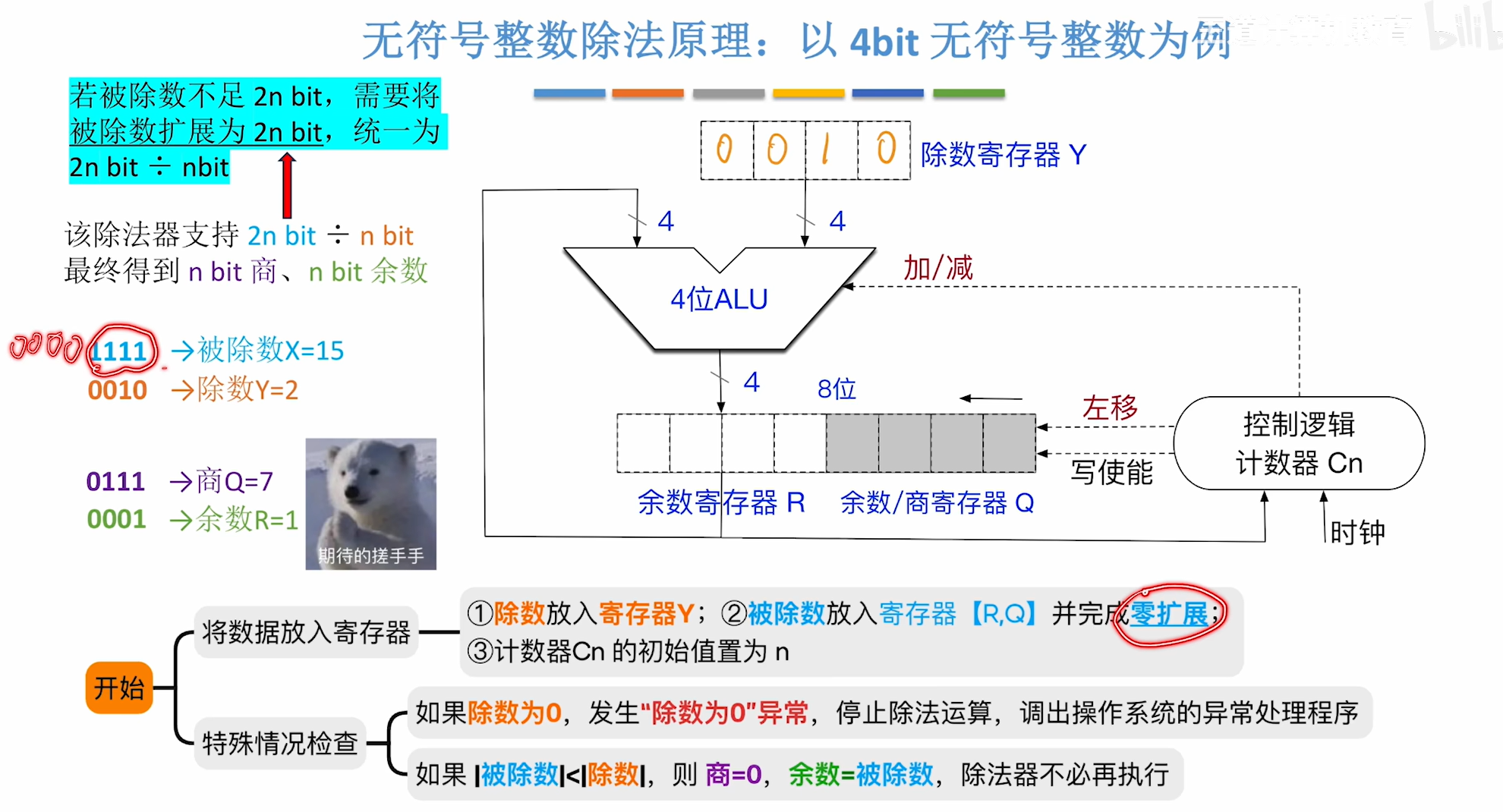
   • 将被除数放入寄存器RQ后，若高位不足，则进行零扩展
2. 计算：
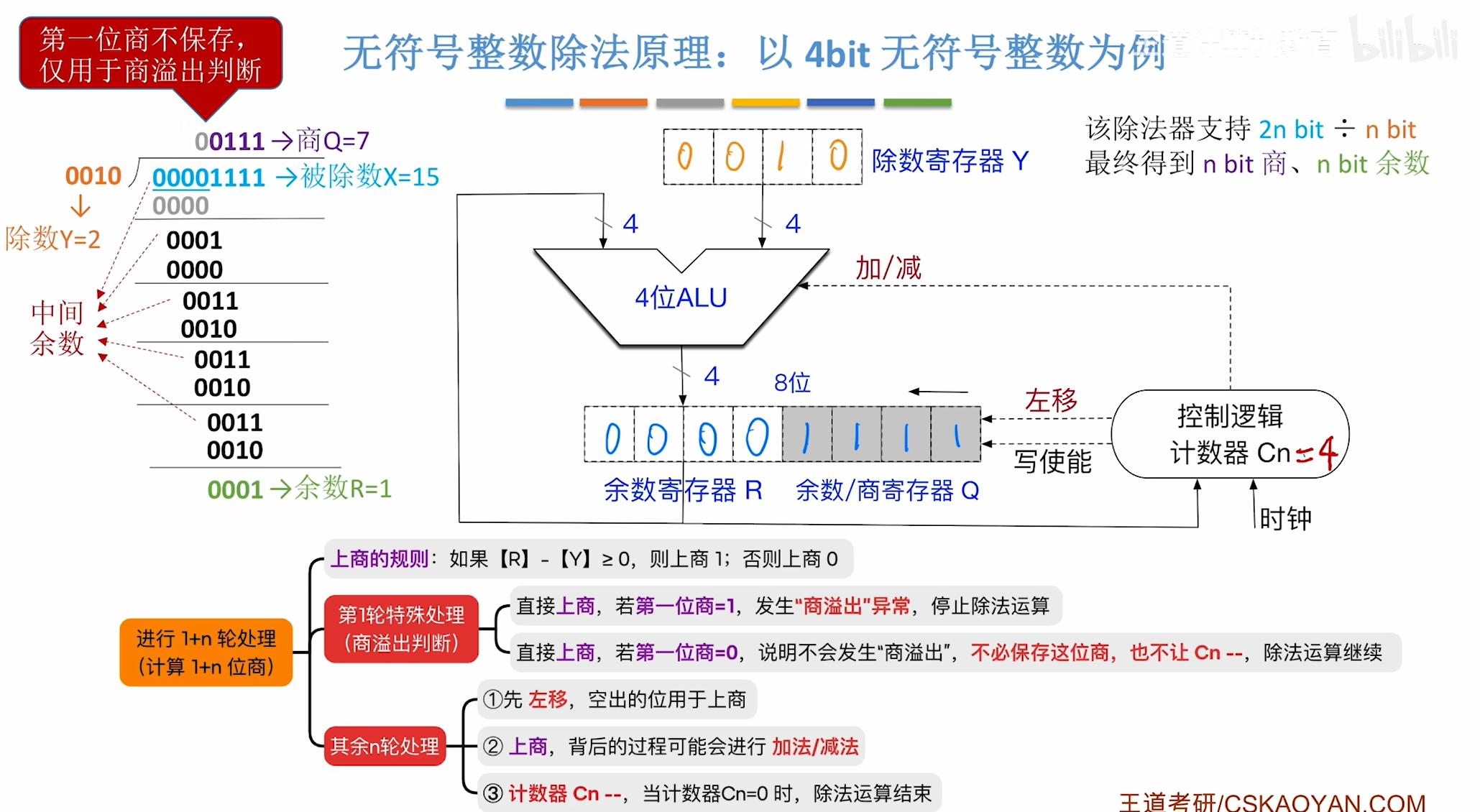
   • 为什么用第一位商判断溢出？因为最终运算结果仅保留低n位，第一位商仅与高n位有关，所以用于判断溢出
   • 将R-Y的值写入寄存器R中，判断上商值：
     1. 若上商值为0，则原先不应对寄存器R中的值进行更改，故将R-Y加上Y后存入R，恢复寄存器R中原先储存的值
     2. 若上商值为1，则中间余数结果正确，余数寄存器R中存储R-Y正是我们期待的结果，所以不进行修改

TIP

最终得到：n bit 寄存器R 保存余数，n bit 寄存器Q 保存商

关于“商溢出”问题的进一步探讨

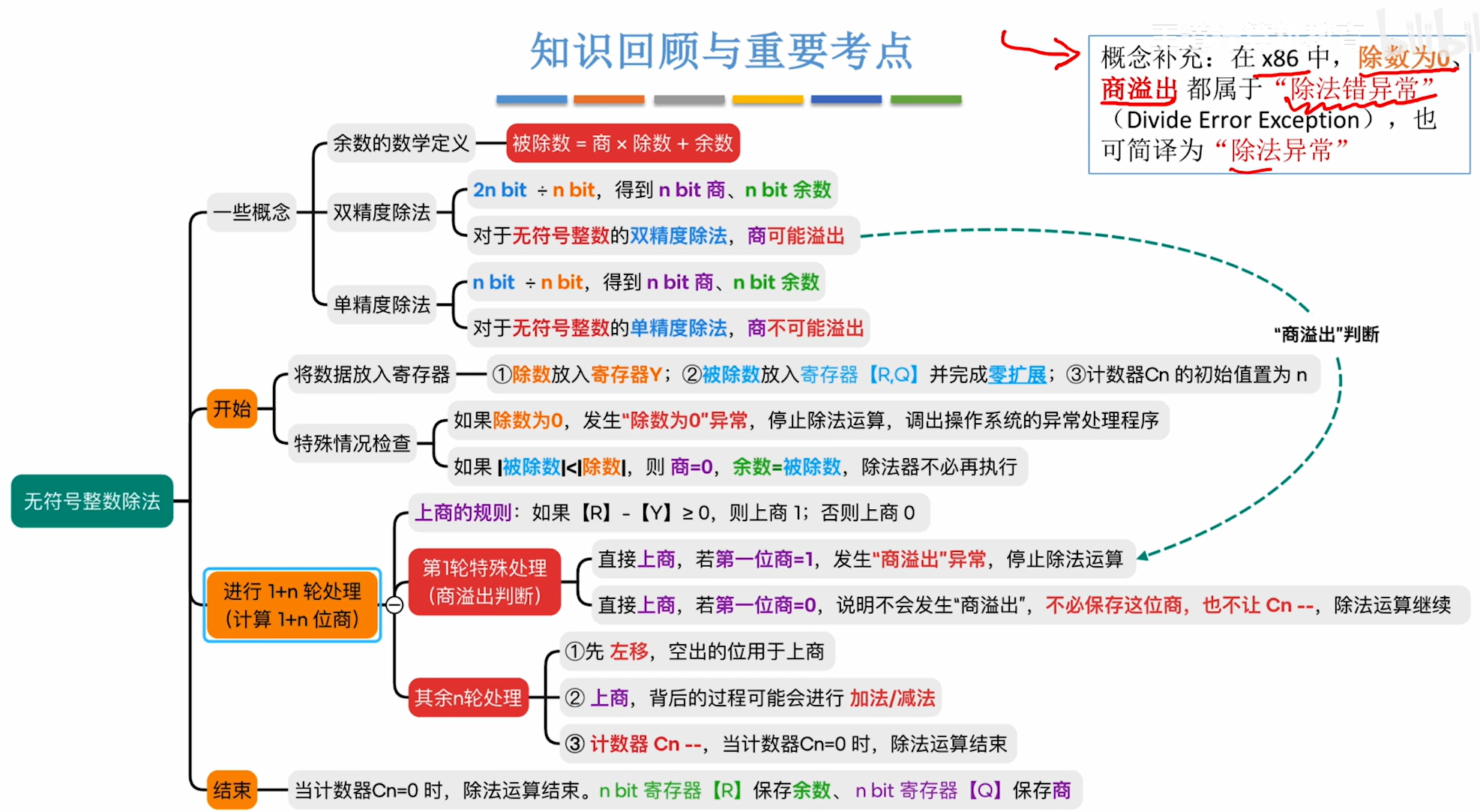
该除法器运算器支持： 2n bit ÷ n bit （双精度除法）（被除数原本就有nbit） n bit ÷ n bit （单精度除法）（被除数原本只有nbit，需要统一为2n bit ÷ n bit，对被除数进行位扩展） 这两种除法最终都仅保留 n bit 商、 n bit 余数 例：

实际上：

1. 2n bit ÷ n bit，商的实际位数可能超过 n bit，因此，无符号整数的双精度除法可能发生“商溢出”（因为最终仅保留 n bit 作为最终结果）
2. n bit ÷ n bit，商的实际位数不可能超过 n bit，因此，无符号整数的单精度除法不可能发生“商溢出”

重要考点及回顾

概念补充

在x86中，除数为0、商溢出都属于“除法错误异常”，也可简称为"除法异常"

贡献者

freeway348

文件历史

最后编辑于 10 天前查看完整历史

74226-Create 抓阄原理.md