2. 定点数的编码表示（原码、反码、补码、移码）

字数

1614 字

阅读时间

7 分钟

---

真值0的表现形式

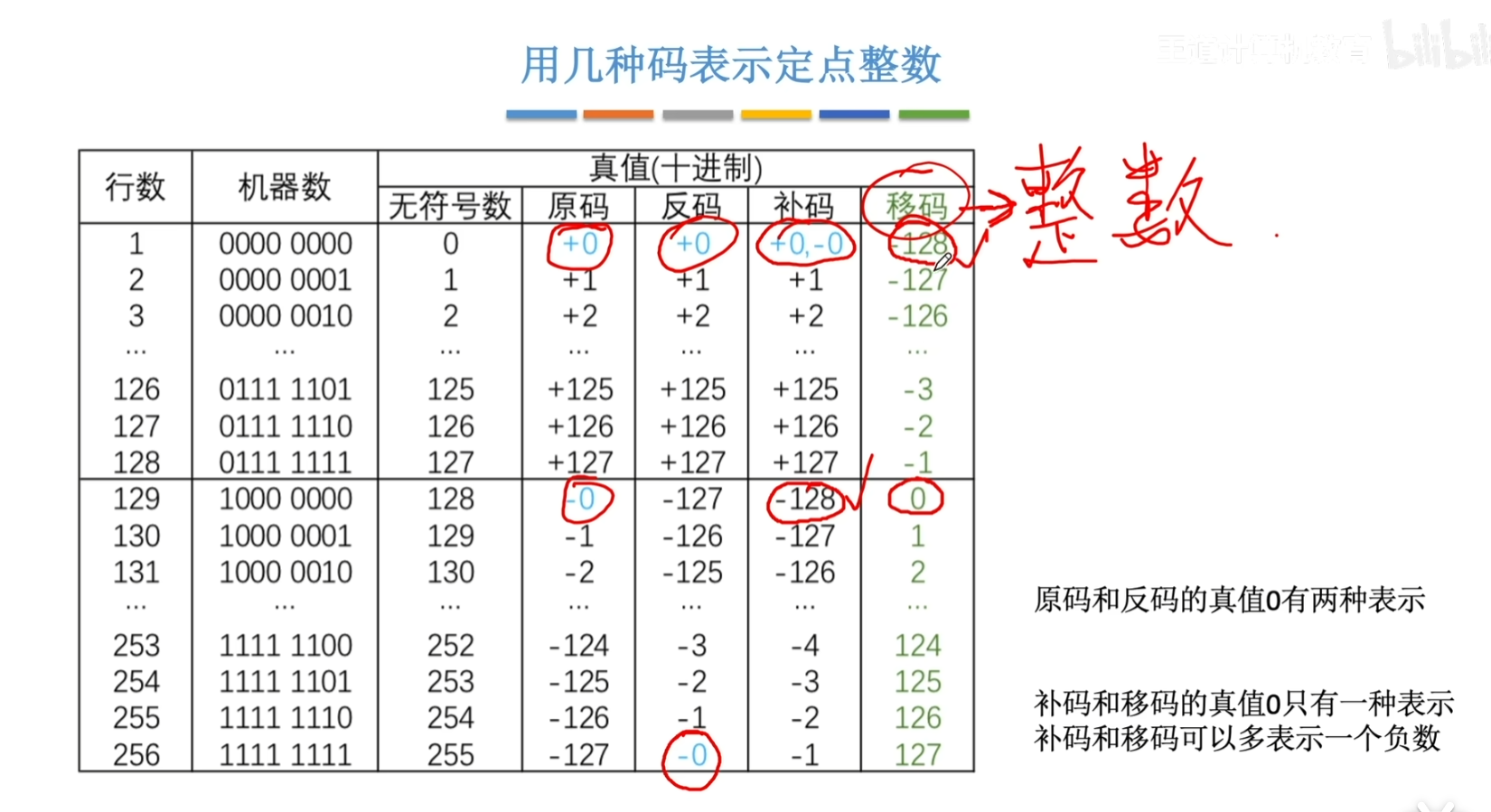
真值0在原码中有两种形式：+0和-0

移码的重要作用

反码是原码转为移码的一个中间状态

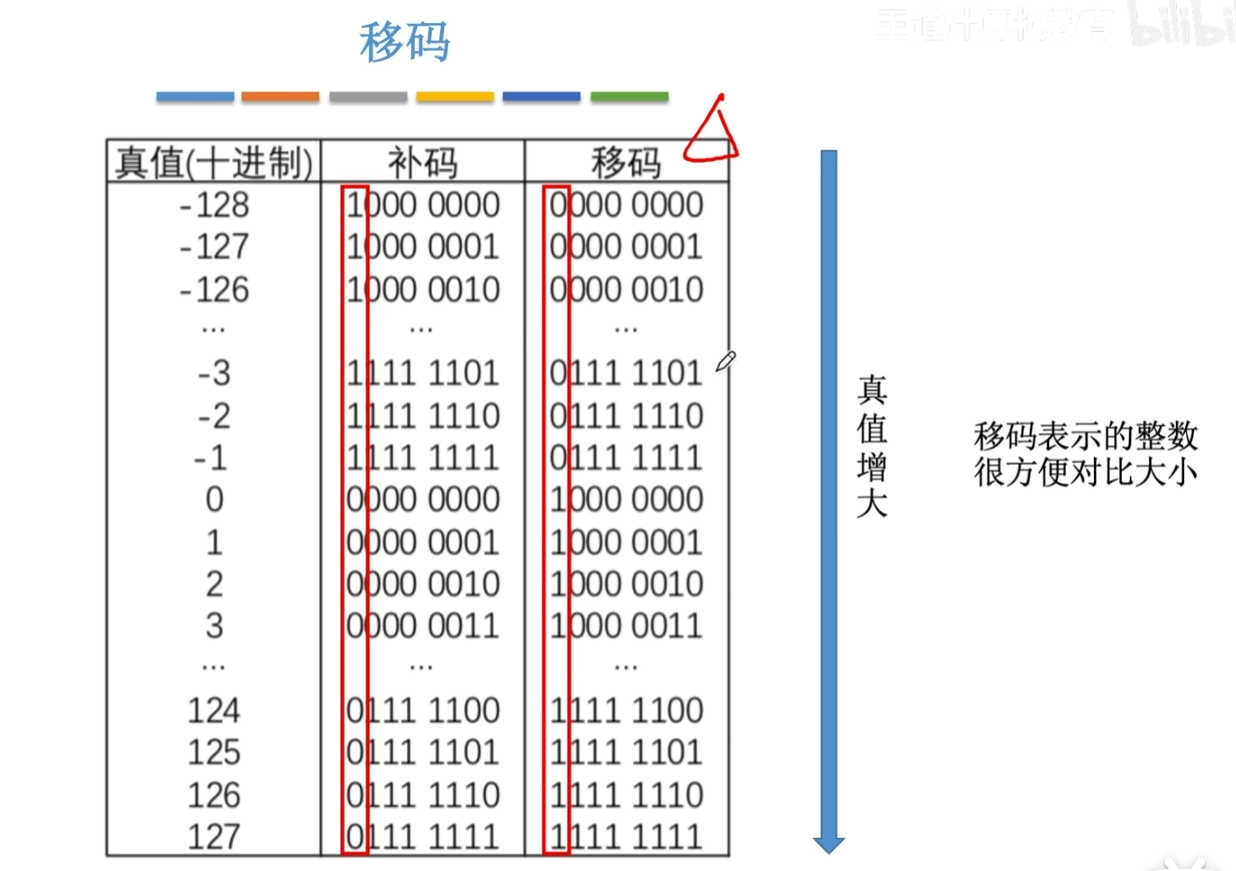当真值递增时，移码的数值位也是递增的，所以可以用移码来快速便捷地比较真值的大小

🌟🌟🌟重点总结

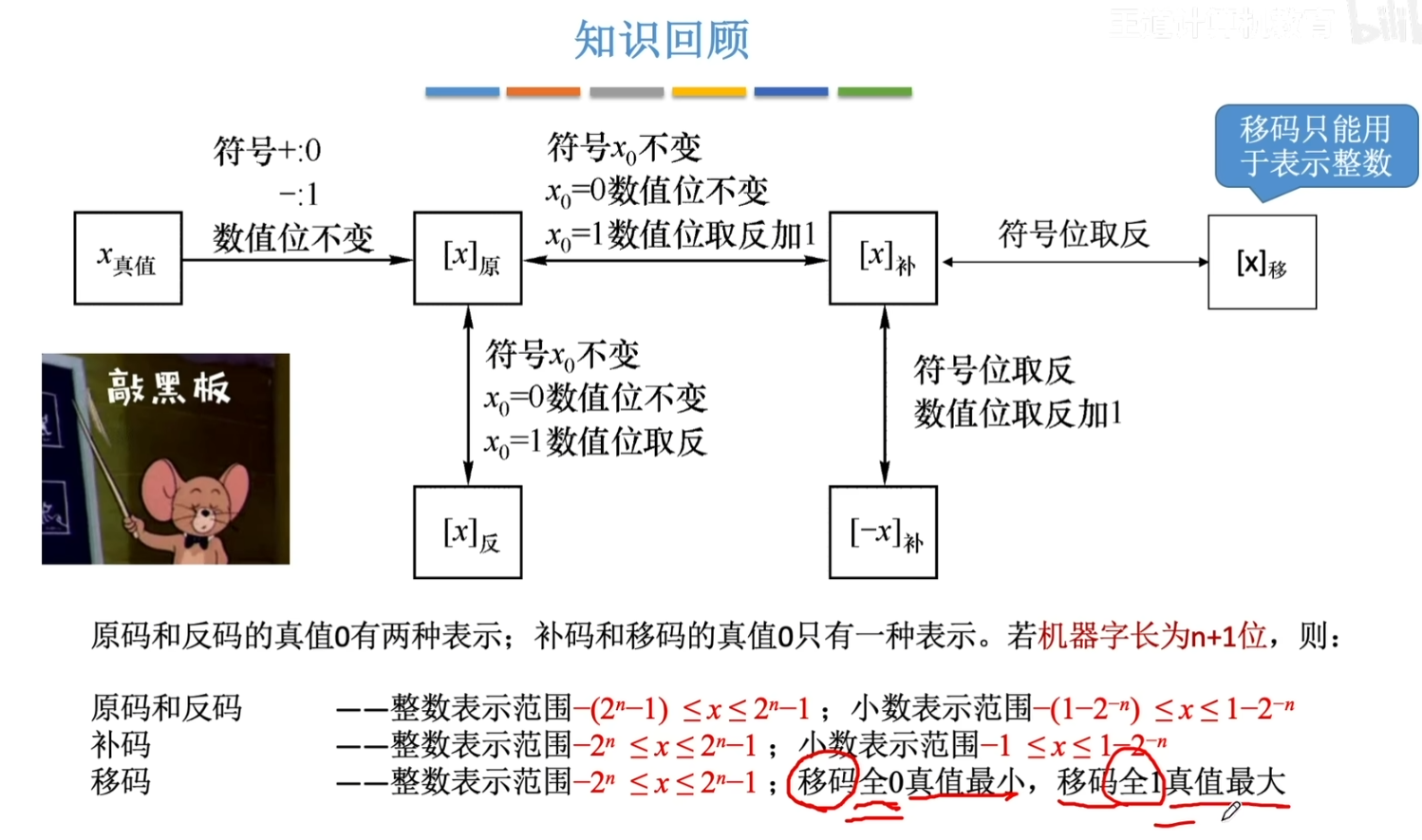
补码和移码的真值0均不区分符号，不能用+0或-0来表示，只能使用0来表示

TIP

补码的补码=原码

• 假设机器数一共有n位：^[1]
  1. 原码的权值理解：最高位为符号位，其余位权值从小到大，从右到左，分别为：$2^0,2^1,2^2,...,2^{n-2}$
  2. 🌟🌟🌟 补码的权值理解：最高位权值为 $-2^{n-1}$， 其余位权值从小到大，从右到左，分别为：$2^0,2^1,2^2,...,2^{n-2}$ （按该理解，以补码形式表现的机器数，若使用该位权理解进行计算，则最终得到的结果即为真值？）
  3. 🌟🌟🌟移码（偏置值）：$[x{]}_{\mathrm{移}}=x+\mathrm{偏}\mathrm{置}\mathrm{值}$ （偏置值一般写作$2^n$ 或 $2^{n-1}$，n为表示位数，x表示真值）
  4. 移码的权值理解：最高位权值为 $2^{n-1}$， 其余位权值从小到大，从右到左，分别为：$2^0,2^1,2^2,...,2^{n-2}$，因为移码与补码仅符号位相反，可以结合来记忆

🌟🌟🌟特殊数据的补码表示

尤其牢记(-2^n)的补码

1. $[+0{]}_{\mathrm{补}}=[-0{]}_{\mathrm{补}}=0,00...0$ （含符号位共 n + 1 个0）
2. $[-1{]}_{\mathrm{补}}=2^{n+1}-1=1,11...1$ （含符号位共 n + 1 个1）
3. $[2^n-1{]}_{\mathrm{补}}=0,11...1$ （n个1），即：n+1位补码能表示的最大整数
4. $[-2^n{]}_{\mathrm{补}}=1,00...0$ （n个0），即：n+1位补码能表示的最小整数

原、反、补码与有符号数、无符号数的关系

TIP

只有"有符号数"才存在原、反、补码！！！

整数类型

在C语言中，整数类型都是以补码形式存储在计算机内的，无符号数则没有符号位，无符号数的所有二进制位都表示数值，相当于数的绝对值，即真值

无符号数的补码就是其本身，在计算机内部所有位都按照2进制进行存储，不需要进行任何变换

强制类型转换

强制类型转换的结果是保持二进制各位的值不变，仅改变解释这些位的方式，如：

int main()
{
	short x = -4321;
	unsigned short y = (unsigned short)x;
	cout << "x= " << x << ",   " << "y= " << y << endl;
}

// 最终输出 x = -4321,   y= 61215
// 这里输出的是 x 和 y 的真值，但在计算机内部存储的是它们的补码
// 原先x 在计算机中存储的是补码，将x 的补码复制给y后，由于y是无符号整数，故将得到的该补码视为原码输出
// 将x的所有位均以数值位转换后，得到的结果就是y(y是无符号整数)

int main()
{
	unsigned short x = 65535;
	short y = (short)x;
	cout << "x= " << x << ",   " << "y= " << y << endl;
}
// 输出 x= 65535， y= -1
// 因为 x 是无符号整数，将其转换为有符号整数后赋值给y（x和y的所有位都相同，均为1），y是有符号整数，在计算机内部以补码形式，所以将其输出为真值时需要将该补码转化为原码，由于该补码为负数，故将其所有数值位取反后+1，得到原码：1,0000....00001（中间都是0），输出真值即为-1

当大字长变量向小字长变量赋值时，系统把多余的高位部分直接截断，低位部分直接赋值，如：

int main()
{
	int x = 165537;
	short y = (short)x;
	cout << "x = " << x << ",  " << "y = " << y << endl;
}

// 输出结果：x = 165537, y = -31071
// x，y 的十六进制表示分别为：0x000286a1,0x86a1
// 当 x 强制赋值给 y 时，将高位截断了，仅保留了低位"86a1"

当小字长变量向大字长变量赋值时，无符号整数进行零扩展（在扩展的高位用0补全），有符号整数则进行符号扩展（在扩展后的高位用符号数进行填充补全）

原、反、补码的优缺点

模运算（了解即可）

所以减法是可以用加法来代替的，在 mod 12 的前提下，可以将 -3 用 9 替代 补数：即互补的数，如：-3 和 9 就互为补数，两个补数绝对值之和 = 模 在计算机中，若存在8位机器数，则它的模是 $2^n=2^8=256$模 - a的绝对值 = a 的补数（该补数为正数，可用于将减法替换为加法），也是补码的原生定义 即：a 的补数，就是 a 的补码

作用

正+负=正+$[\text{负}{]}_{\text{补码}}$ 当然，在计算过程中也可将负数的符号位取出，将运算式变为：正+负 =正-正 这两者最终得到的结果都是相同的正确结果 要牢记：不能直接进行正+负的运算

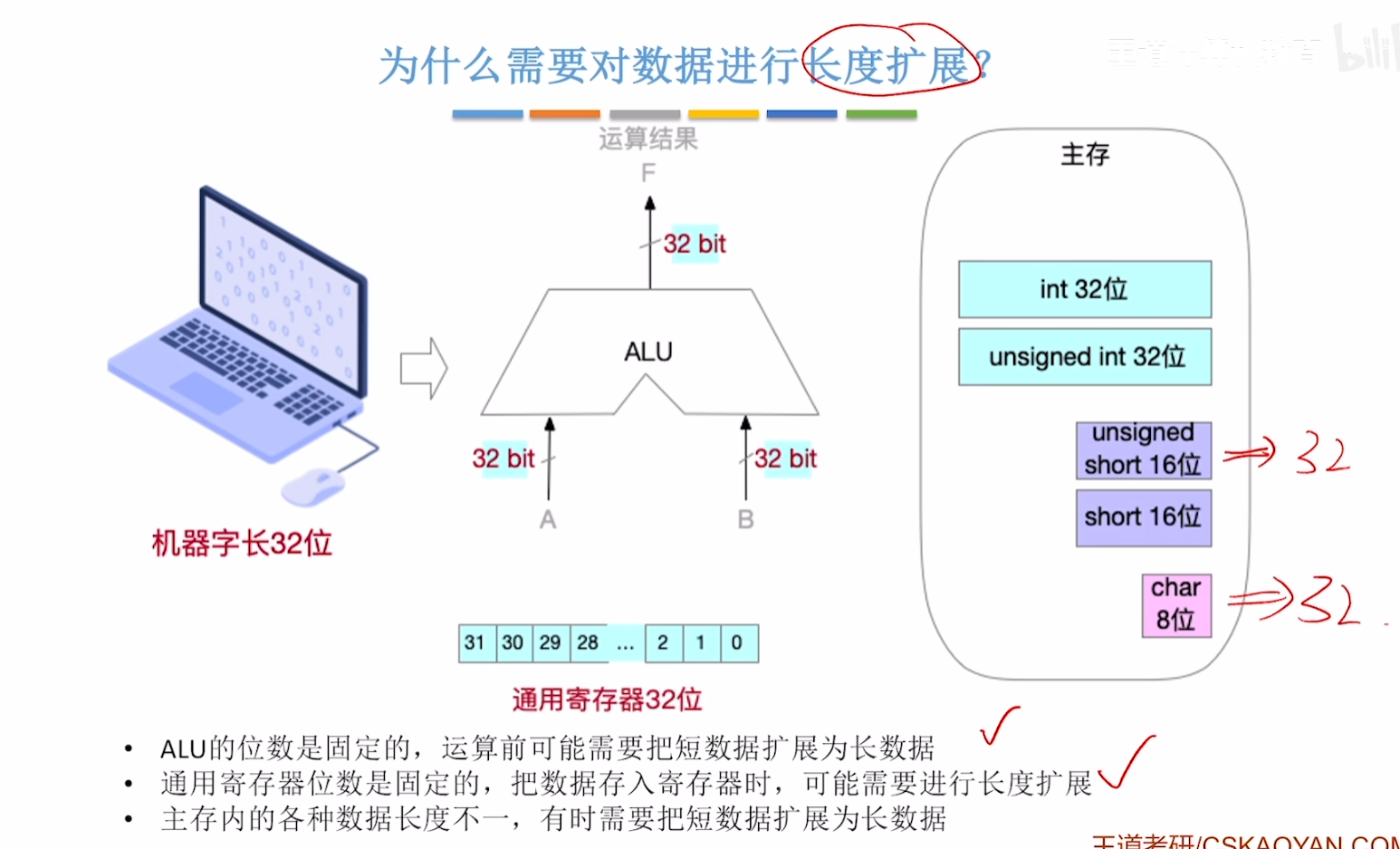
为什么要进行长度扩展？

无符号数的作用（地址表示）

适用场景

一般在全是正数运算且不出现负值结果的场合下，可用无符号数表示，如地址运算地址表示没有负的

特点

1. 无符号数的编码中没有符号位，无符号数总是正数，所以很多时候简称为无符号数
2. 在字长相同的情况下，表示范围大于有符号数

贡献者

freeway348

文件历史

最后编辑于 10 天前查看完整历史

74226-Create 抓阄原理.md

---

1. 非常重要，对移码、补码的权值理解进行深刻记忆理解并熟练运用 ↩︎