一元函数积分的几何应用

字数

1498 字

阅读时间

6 分钟

---

测度：长度、体积、面积
熟悉基础30讲P591~P593的几种常见平面图形，在计算中时常要用到

一、用定积分表达和计算平面图形的面积^[1]

定积分：推广 ---> 可能用到收敛情况下的反常积分
平面图形：
	三大体系下的图形：
		1. 直角坐标系下：直接算
		2. 参数方程下：直接算（情况较少）；换元法（大多数情况）
		3. 极坐标下：直接算
面积：可以推广为用收敛的反常积分进行表示

扇形面积计算公式

1. $S=\frac{n}{360}\pi R^2$， 其中 n 为圆心角，R 为扇形半径
2. $S=\frac{1}{2}lR$，其中 $l$ 为扇形的弧长
3. $S=\frac{1}{2}\theta R^2$，其中$\theta$是以弧度表示的圆心角 弧长 $l=\theta R$

二、用定积分表达和计算旋转体的体积

1. 绕 x 轴旋转

2. 绕 y 轴旋转

"柱壳法"求体积：将截取的一小块（阴影部分）绕 y 轴旋转，可得到一个小的空心圆柱，将其平摊展开，可近似得到右侧的长方体，长为 $2\pi x$ ，宽为 $dx$，高为 $|y(x)|$ （因为绕 y 轴旋转，不一定都是正的，可能是从 y+ 到 y - 都有涉及的图形）

如何判断具体解题是使用绕 x 轴旋转还是绕 y 轴旋转？

• 若所给图形是 y(x) 与 y 轴围成的：
  1. 若要求该图形绕 x 轴旋转的体积，则求出其反函数 $x=\varphi (y)$（将x ，y地位互换），再使用绕 y 轴旋转的体积公式（因为相当于将坐标轴旋转了，x 轴变到了原先 y 轴的位置，还要注意要将公式中的 x 换成 y， y(x) 换成 $\varphi (y)$）
  2. 若要求该图形绕 y 轴旋转的体积，则同理，求出 $x=\varphi (y)$ 后，再使用绕 x 轴旋转的体积公式即可

TIP

先来看做法：若函数y(x)与x轴围成图形，则若该图形绕x轴旋转，则使用绕x轴旋转的公式，否则使用绕y轴旋转的公式；若是y(x)与y轴围成图形，则该图形绕y轴旋转，则使用绕x轴旋转公式，否则使用绕y轴旋转的公式，记得变换公式中x和y的位置 本质上是这样：若函数y(x)与某一坐标轴围成图形，则若要绕该坐标轴旋转，则使用绕x轴旋转的公式；若要绕另一坐标轴进行旋转，则使用绕y轴旋转的公式，必须要注意公式的字母是否正确

3. 平面曲线绕直线旋转

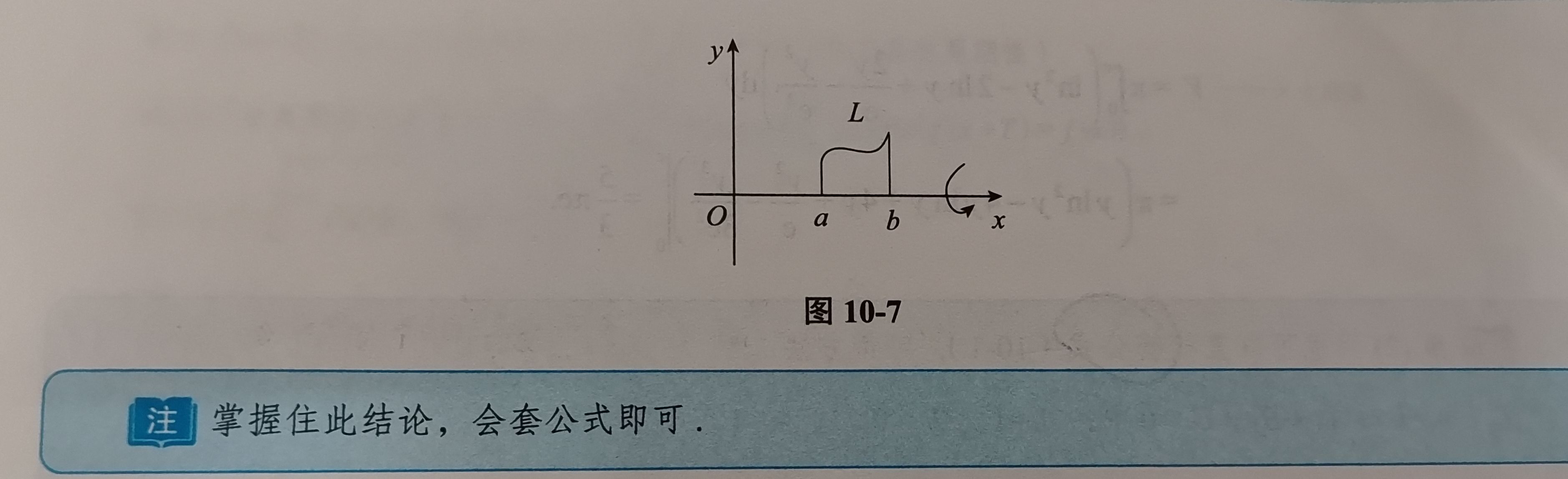
三、用定积分表达和计算函数的平均值

设 $x\in [a,b]$ ，函数 $y(x)$ 在 $[a,b]$ 上的平均值为 $\bar{y}=\frac{1}{b-a}{\int }_a^{b}y(x)dx\Rightarrow \bar{y}=y(\xi ),\xi \in [a,b]$

四、其他几何应用

1. “平面上的曲边梯形”的形心坐标公式

什么是形心？形心就是物体中所有点的平均位置，也可以说是面的形心就是截面图形的几何中心

计算公式： 直接记住最终的公式即可，目前还没学二重积分，所以不用纠结公式是怎么来的

2. 平面曲线的弧长

1. 若平面光滑曲线由直角坐标系方程 $y=y(x)(a\le x\le b)$ 给出，则 $s={\int }_a^b\sqrt{1+[y\prime (x){]}^2}dx$
2. 若平面光滑曲线由参数方程 $x=x(t),y=y(t)(\alpha \le t\le \beta )$ 给出，则 $s={\int }_{\alpha }^{\beta }\sqrt{[x\prime (t){]}^2+[y\prime (t){]}^2}dt$
3. 若平面光滑曲线由极坐标方程 $r=r(\theta )(\alpha \le \theta \le \beta )$ 给出，则 $s={\int }_{\alpha }^{\beta }\sqrt{[r(\theta ){]}^2+[r\prime (\theta ){]}^2}d\theta$

• 基本微元计算公式：$ds=\sqrt{(dx{)}^2+(dy{)}^2}$
  • 其中，$ds$ 是弧微分，所以 $s={\int }_a^b\sqrt{(dx{)}^2+(dy{)}^2}$ ，其他公式都是由该微分公式衍生推算出的

3. 旋转曲面的面积（侧面积）

注意事项！！！

1. 注意与体积公式进行区分
2. 注意该侧面积求的是绕 x 轴旋转所得的旋转曲面面积

实际上，所有公式都是由侧面积的基本公式 $S={\int }_a^{b}2\pi |f(x)|ds$ 变形而来

为什么求旋转体体积使用的是dx，而求侧面积就必须使用ds（ds是弧微分，即平面曲线弧长的微元），因为求旋转体体积时使用的是$[a,b]$区间的面积，微元法求的是区间dx；而求侧面积时，使用微元法，我们发现阴影部分面积为如下形式：$2\pi f(x)ds$，当ds非常非常小的时候，可以将该面积看做一个长方形来求解，此处的是ds而不是dx是因为我们要用到的是曲面的弧长，而不是区间长度

4. 平行截面面积为已知的立体体积

如图，在区间 $[a,b]$ 上，垂直于 x 轴的平面截立体 $\mathrm{\Omega }$ 所得到的截面面积为 x 的连续函数 $A(x)$，取体积微元：$dV=A(x)dx$，则 $\mathrm{\Omega }$ 的体积为：$V={\int }_a^{b}A(x)dx$ 若某平面截立体并未垂直于x轴，则需要求出其截面面积 $\alpha A(x)$ ，然后代入体积公式

• 为什么说旋转体体积是其特例？因为该已知平行截面面积的立体体积，可看做是某一函数 $g(x)$ 绕某一曲线 $p(x)$ 旋转得到的

贡献者

freeway348

文件历史

最后编辑于 10 天前查看完整历史

74226-Create 抓阄原理.md

---

1. 及时回看，以免遗忘 ↩︎