2. 做题技巧
字数
701 字
阅读时间
3 分钟
一、泰勒展开的妙用
导数相关大题思路
首先联想到导数在某点的定义,泰勒展开式,拉格朗日定理,罗尔定理等相关公式,再根据每个公式定理的性质与形式来判断使用哪个
- 当遇到需求二阶导甚至三阶导的大题时(一般仅到二阶导),但却仅给出原函数的部分条件,最终要求证明有关一阶导的结论,此时应当使用泰勒展开
- 已知在点
处的泰勒展开公式为: ,需要几项就写几项,若仅需求二阶导与原函数和一阶导的关系,则仅列举到二阶,其中,二阶项为拉格朗日余项,即: - 此处使用带拉格朗日余项的泰勒公式,具体使用带佩亚诺余项的泰勒公式还是拉格朗日的泰勒公式,都需要根据具体情况判断,但大多数情况下,仍较多使用带拉格朗日余项的泰勒公式
- 泰勒展开后,若题目已给出原函数的特殊点和二阶导函数的不等式关系,则可考虑特殊点代入
后,联立方程求解;若无法求得解,或是无法继续计算,则考虑另一条思路:即 将特殊点代入 x,使得原泰勒公式方程变为,随后联立方程组必能求出解 - 该变换后的泰勒公式可看作是在区间内一点
进行泰勒展开,并对其附近的近值点 进行分析 - 带拉格朗日余项的一阶泰勒公式(最高阶为一阶)就是拉格朗日定理 例:

- 该变换后的泰勒公式可看作是在区间内一点
- 已知在点
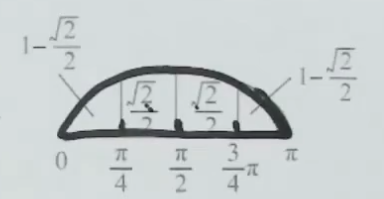
二、常用图像面积
的一拱面积为2 示意图: