2.2.3 定点数的加减运算

字数

1089 字

阅读时间

5 分钟

---

一、定点数的加减运算

1. 原码的加减运算（了解即可）

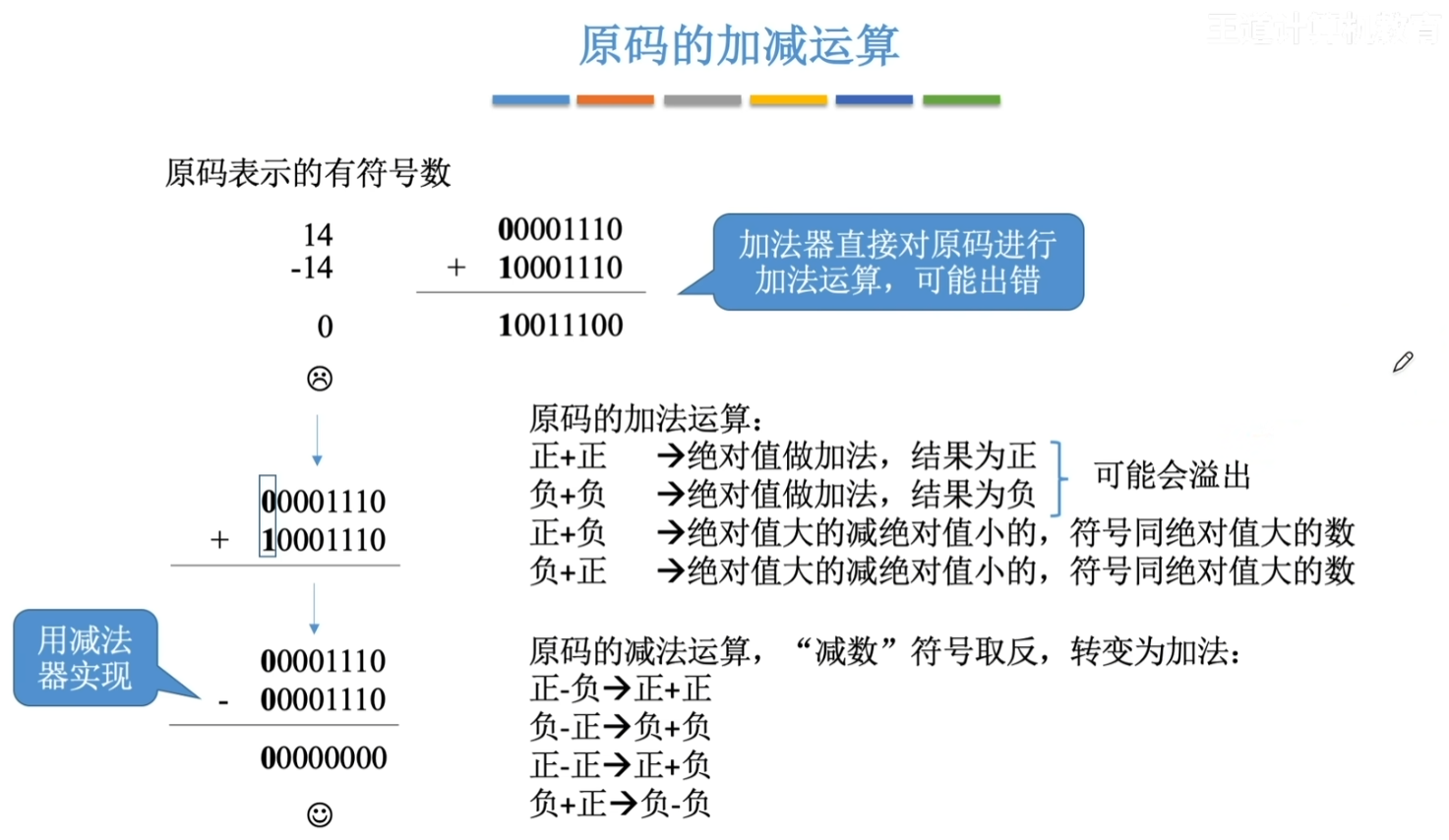只有当"正+正"或"负+负"时才可能发生溢出（最高数值位发生进位，导致符号位改变）

但计算机中通常使用补码进行计算，所以对原码的计算仅作了解即可

2. 补码的加减运算

(1)补码的加减运算基本公式

• 补码加减运算的公式：（设机器字长为 n+1 ）
  1. $[A+B{]}_{\mathrm{补}}=[A{]}_{\mathrm{补}}+[B{]}_{\mathrm{补}}(mod{2}^{n+1})$
  2. $[A-B{]}_{\mathrm{补}}=[A{]}_{\mathrm{补}}+[-B{]}_{\mathrm{补}}(mod{2}^{n+1})$
• 特点：
  1. 按二进制运算规则进行，逢二进一
  2. 遇到加减法按公式计算
  3. 符号位与数值位一起参与运算，运算结果的符号位也在运算中直接得出
  4. 最终运算结果的高位丢弃，保留n+1位，运算结果也是补码

(2)补码的溢出判断

• 前提：当且仅当两个符号相同的数相加或两个符号相反的数相减时才可能发生溢出（A-B可看作A+(-B)，所以也可记住，符号相同的两数相加就可能发生溢出）
  • 即：只有"正数+正数"才会发生上溢：正+正=负；只有"负数+负数"才可能发生下溢：负+负=正 🌟补码的加减溢出判断有三种方式：^[1]

a. 采用一位符号位（又称模2补码）

设A的符号为$A_S$，B的符号为$B_S$，运算结果的符号为$S_S$，则溢出逻辑表达式为：$V=A_S{B}_S\overline{S_S}+\overline{A_S}\overline{B_S}{S}_S$ 若V=0，则表示无溢出，若V=1，则表示有溢出

b. 采用双符号位

该方法实际存储时仅存储了 1 个符号位，运算时会复制一个符号位
正数：+ 的符号位为：00，
负数：- 的符号位为：11，

双符号位法也称为模4补码（仅保留位权<4的位，即：$2^1,2^0$ 这两位，也就是说符号位有2位）

• 符号位$S_{s1}{S}_{s2}$ 的各种情况如下：
  1. $S_{s1}{S}_{s2}$ = 00：表示结果为正数，无溢出
  2. $S_{s1}{S}_{s2}$ = 01：表示结果正溢出
  3. $S_{s1}{S}_{s2}$ = 10：表示结果负溢出
  4. $S_{s1}{S}_{s2}$ = 11：表示结果为负数，无溢出

第一个符号位$S_{s1}$ 表示运算正确时应该得到的符号位，第二个符号位$S_{s2}$ 表示实际运算得到的符号位，若这两个符号位不同，则发生溢出，即：溢出逻辑判断表达式为：$V=S_{s1}\oplus S_{s2}$
若V=0，则表示无溢出，若V=1，则表示有溢出

c. 采用一位符号位根据数值位的进位情况判断溢出

用$C_n$ 表示符号位（最高位）的进位，用 $C_{n-1}$ 表示最高数值位（次高位）的进位

溢出逻辑表达式为：$V=C_n\oplus C_{n-1}$ 若V=0，则表示无溢出，若V=1，则表示有溢出 简单记忆：若最高位与次高位的进位不同，则发生溢出

二、无符号数的加减运算

加法

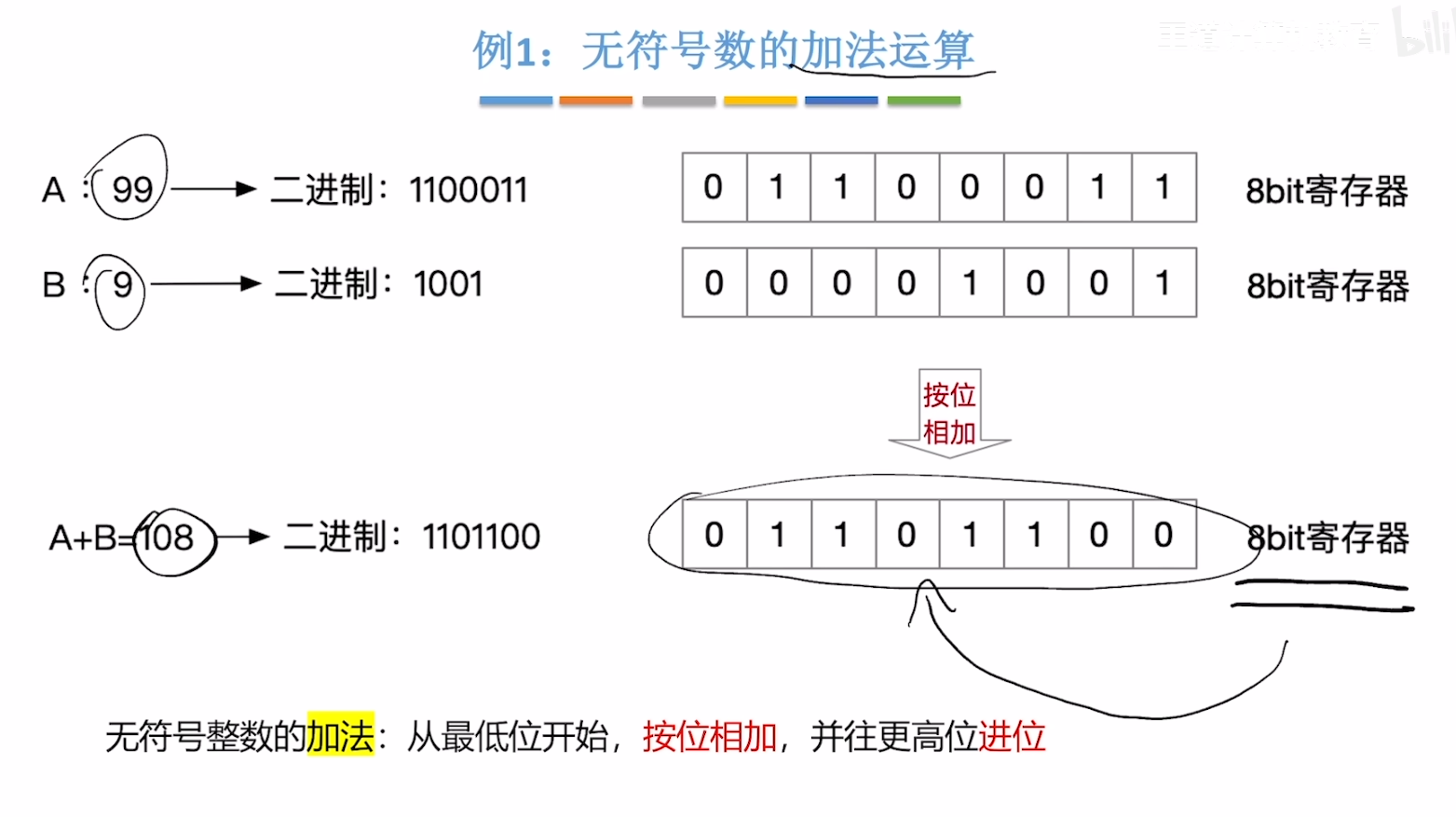
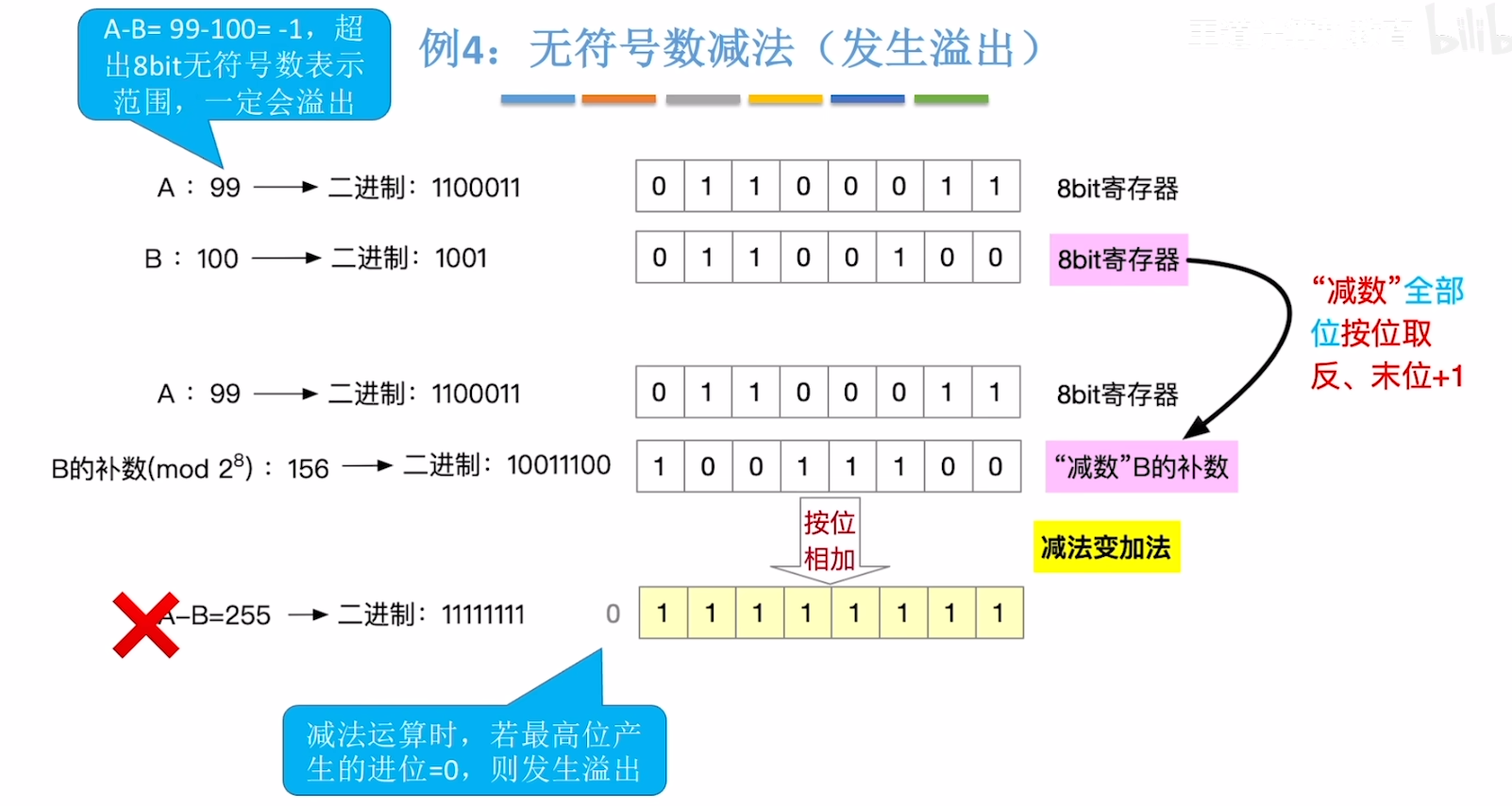
减法

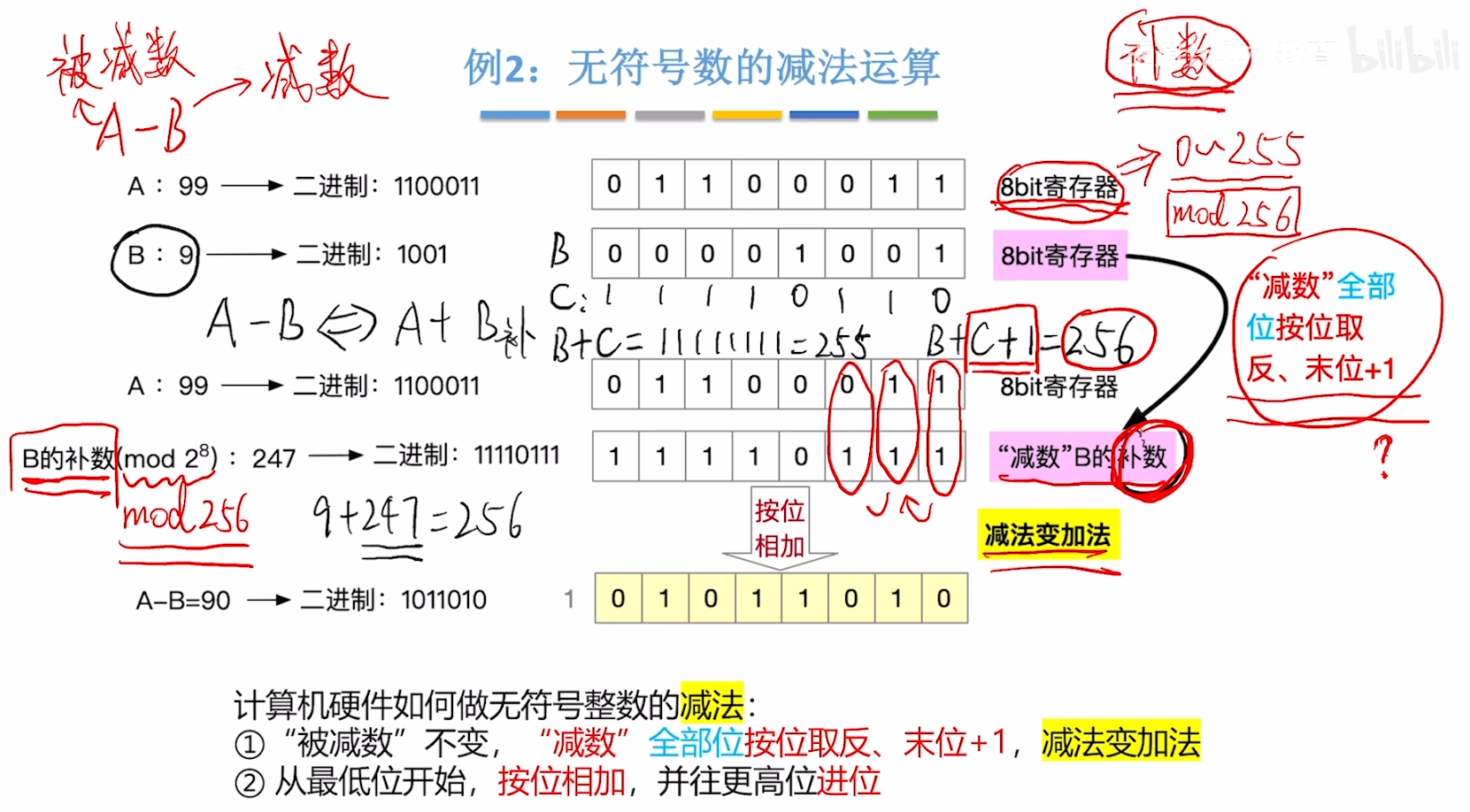
在 8 位寄存器中，数值最多能表示 0 ~ 255，也就是 mod 256，那么假设在该寄存器中存储了一个数A，则 $A+[A{]}_{\text{补}}=256$ 无符号数求补数：全部位取反后 + 1 假设将 A 取反后得到 B，则 A + B = 255 必定成立，故 + 1 即可得到 256

溢出判断

考试遇到判断无符号数溢出问题，一般使用手算方法，而计算机内部判断无符号数加减是否溢出的方法就如红蓝两行所述

加法溢出判断

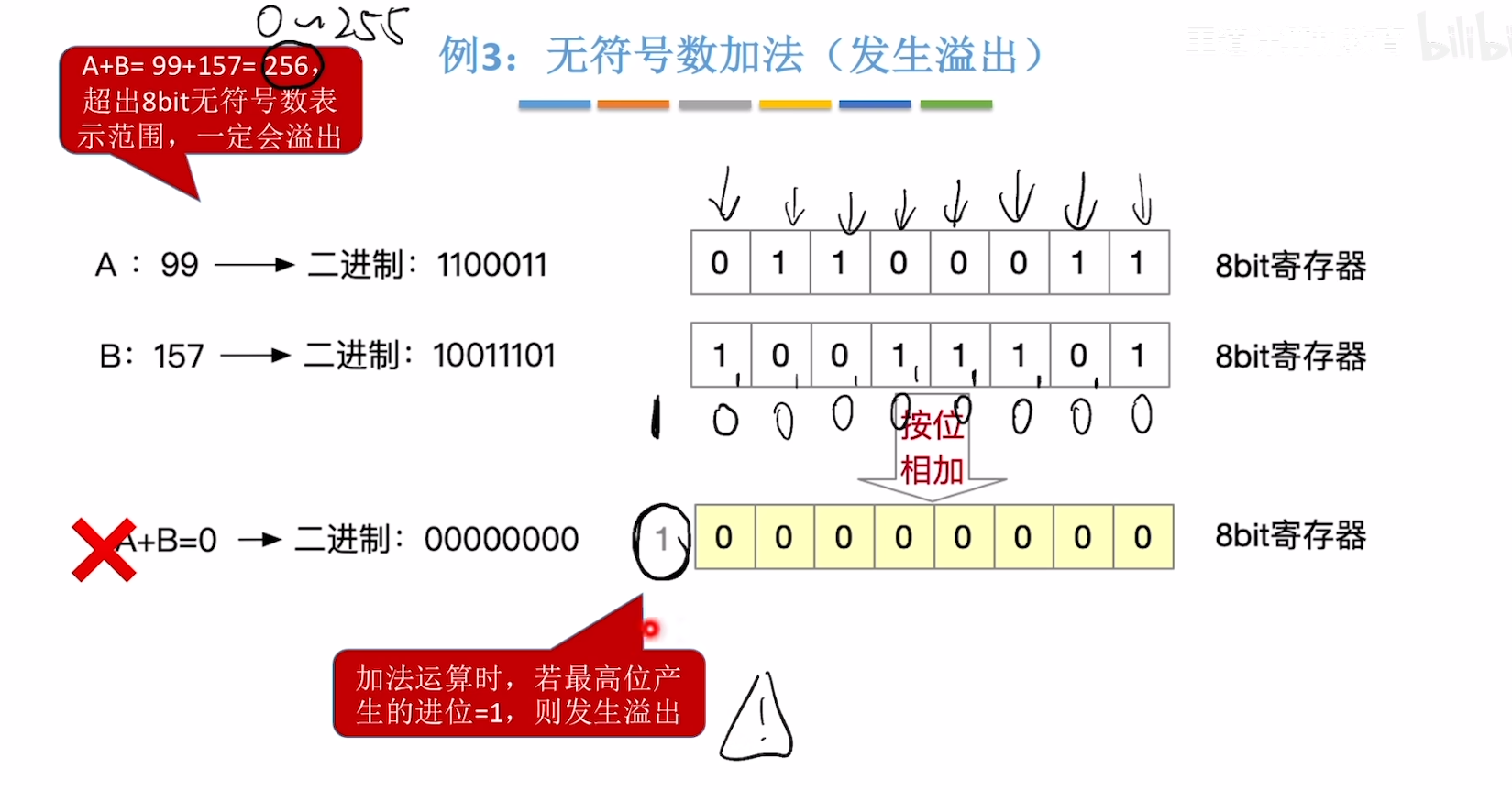
减法溢出判断

同样的，按减法运算进行计算，若按位相加后，最高位进位为0，则发生溢出

贡献者

freeway348

文件历史

最后编辑于 10 天前查看完整历史

74226-Create 抓阄原理.md

---

1. 重点记忆：有符号整数补码的三种溢出判断 ↩︎