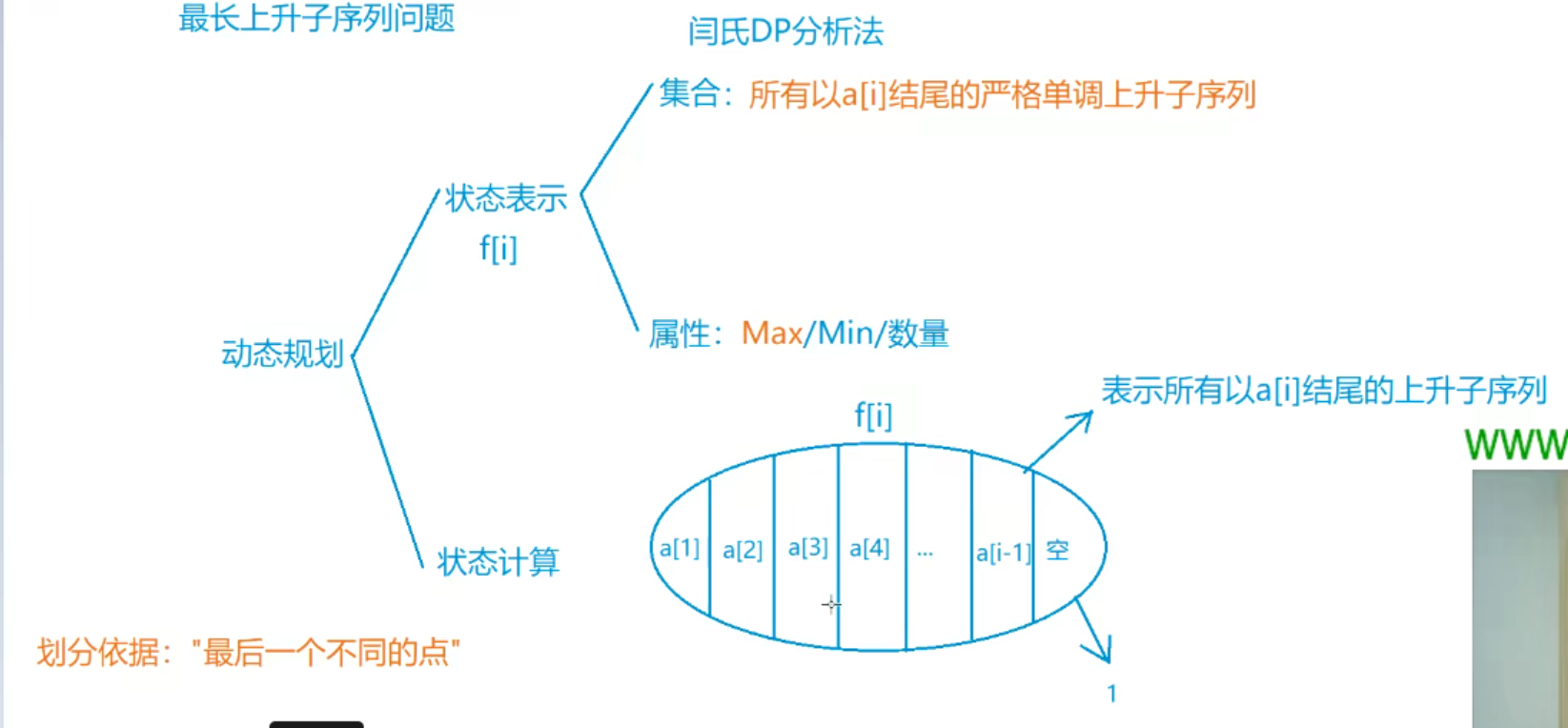
最长上升子序列

字数

616 字

阅读时间

3 分钟

---

例题

最长上升子序列

代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 5010;
int n;
int f[N]; // f[i]：以第 i 个数结尾的序列中，最长上升子序列的长度
int a[N];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++)
        cin >> a[i];
    for (int i = 1; i <= n; i ++)
    {
        f[i] = 1; // 先讨论 a[i] 之前没有比 a[i] 更大的数的情况
        for (int j = 1; j < i; j ++) // 再从头讨论倒数第二个不相同的值为 f[j] 的情况
            if (a[i] > a[j])
                f[i] = max(f[i], f[j] + 1);
    }

    int res = 0;
    for (int i = 1; i <= n; i ++)
        res = max(res, f[i]);
    cout << res << endl;
    return 0;
}

友好城市

思路：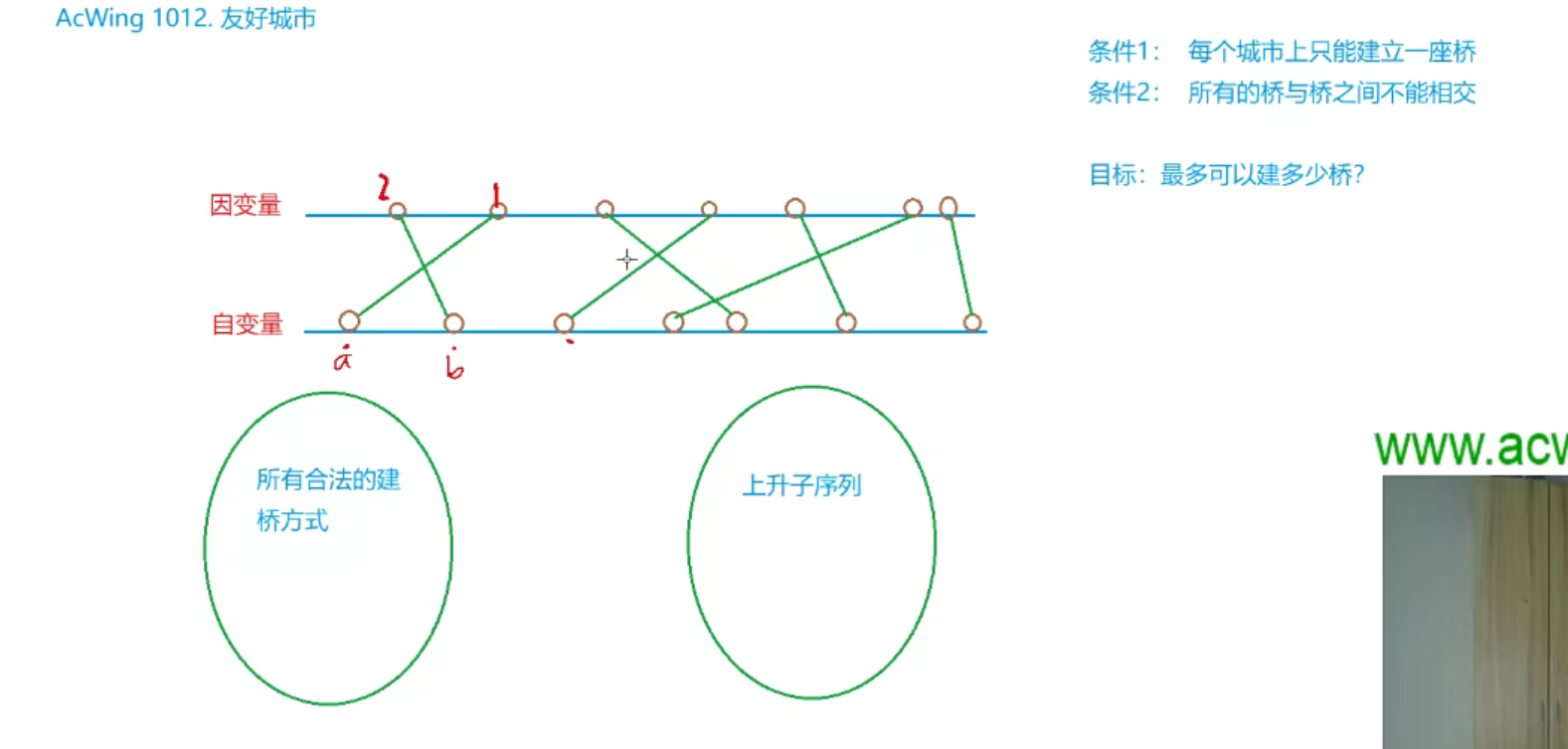

• 使用pair来存储南北两岸建立通路的两友好城市

在数据量大时，需要考虑$O(nlog(n))$ 的做法，可将for循环查找优化为二分查找即可实现

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 2e5 + 10; // 数据量大，需要使用 O(nlog(n)) 的做法
typedef pair<int, int> PII;
int n;
PII g[N];
int f[N];
int q[N];

bool cmp(PII a, PII b) // 重写cmp函数，仅比较first
{
    return a.first < b.first; // first 从小到大排序
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++)
    {
        cin >> g[i].first >> g[i].second;
    }

    // 可不重写，因为每个城市仅有一个友好城市，且互不相同，故不用考虑first相同的情况
    sort(g + 1, g + n + 1, cmp); // 默认排序：first从小到大，first相同时，second从小到大

    int len = 0;
    q[0] = -1;
    for (int i = 1; i <= n; i ++)  
    {   
        int l = 0, r = len; // 因为查找的是上升子序列，即：q[N] 数组中的元素，所以 l 从 0 开始
        while(l < r) // 找到最长上升子序列中小于南岸序号的最大值
        {
            int mid = l + r  + 1 >> 1;
            if (q[mid] < g[i].second) l = mid; // 找到最长上升子序列中小于g[i].second 的最大值，再将 g[i].second 加入到最长上升子序列中
            else r = mid - 1;
        }
        len = max(len, r + 1);
        q[r + 1] = g[i].second;
    }

    cout << len << endl;
    return 0;
}

导弹拦截系统

可能用最长不增子序列，也可能用最长不减子序列，两者结合使用也有可能，所以要对所有情况进行爆搜（dfs）

• dfs 求最小步数问题，一般有两种做法：1. 记一个全局变量最小值，2. 迭代加深

贡献者

freeway348

文件历史

最后编辑于 大约 15 小时前查看完整历史

3b507-algoA

abe72-math